


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-12-2020
Date: 6-1-2020
Date: 8-9-2020
|
The Mertens constant 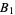 , also known as the Hadamard-de la Vallee-Poussin constant, prime reciprocal constant (Bach and Shallit 1996, p. 234), or Kronecker's constant (Schroeder 1997), is a constant related to the twin primes constant and that appears in Mertens' second theorem,
, also known as the Hadamard-de la Vallee-Poussin constant, prime reciprocal constant (Bach and Shallit 1996, p. 234), or Kronecker's constant (Schroeder 1997), is a constant related to the twin primes constant and that appears in Mertens' second theorem,
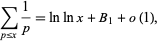 |
(1) |
where the sum is over primes and 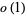 is a Landau symbol. This sum is the analog of
is a Landau symbol. This sum is the analog of
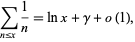 |
(2) |
where 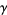 is the Euler-Mascheroni constant (Gourdon and Sebah).
is the Euler-Mascheroni constant (Gourdon and Sebah).
The constant is given by the infinite sum
![B_1=gamma+sum_(k=1)^infty[ln(1-p_k^(-1))+1/(p_k)]](https://mathworld.wolfram.com/images/equations/MertensConstant/NumberedEquation3.gif) |
(3) |
where 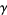 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 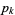 is the
is the 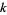 th prime (Rosser and Schoenfeld 1962; Hardy and Wright 1979; Le Lionnais 1983; Ellison and Ellison 1985), or by the limit
th prime (Rosser and Schoenfeld 1962; Hardy and Wright 1979; Le Lionnais 1983; Ellison and Ellison 1985), or by the limit
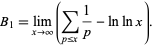 |
(4) |
According to Lindqvist and Peetre (1997), this was shown independently by Meissel in 1866 and Mertens (1874). Formula (3) is equivalent to
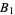 |
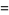 |
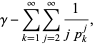 |
(5) |
 |
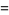 |
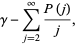 |
(6) |
where 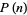 is the prime zeta function, which follows from (5) using the Mercator series for
is the prime zeta function, which follows from (5) using the Mercator series for 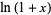 with
with 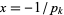 .
. 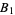 is also given by the rapidly converging series
is also given by the rapidly converging series
![B_1=gamma+sum_(m=2)^infty(mu(m))/mln[zeta(m)],](https://mathworld.wolfram.com/images/equations/MertensConstant/NumberedEquation5.gif) |
(7) |
where 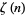 is the Riemann zeta function, and
is the Riemann zeta function, and 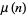 is the Möbius function (Flajolet and Vardi 1996, Schroeder 1997, Knuth 1998).
is the Möbius function (Flajolet and Vardi 1996, Schroeder 1997, Knuth 1998).
The Mertens constant has the numerical value
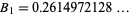 |
(8) |
(OEIS A077761). Knuth (1998) gives 40 digits of 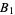 , and Gourdon and Sebah give 100 digits.
, and Gourdon and Sebah give 100 digits.
The product of 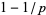 behaves asymptotically as
behaves asymptotically as
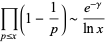 |
(9) |
(Hardy 1999, p. 57), where 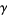 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 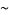 is asymptotic notation, which is the Mertens theorem.
is asymptotic notation, which is the Mertens theorem.
The constant 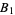 also occurs in the summatory function of the number of distinct prime factors
also occurs in the summatory function of the number of distinct prime factors 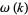 ,
,
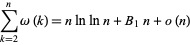 |
(10) |
(Hardy and Wright 1979, p. 355).
The related constant
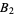 |
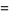 |
![gamma+sum_(k=1)^(infty)[ln(1-p_k^(-1))+1/(p_k-1)]](https://mathworld.wolfram.com/images/equations/MertensConstant/Inline27.gif) |
(11) |
 |
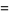 |
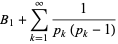 |
(12) |
 |
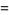 |
![gamma+sum_(n=2)^(infty)(phi(n)ln[zeta(n)])/n](https://mathworld.wolfram.com/images/equations/MertensConstant/Inline33.gif) |
(13) |
 |
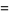 |
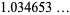 |
(14) |
(OEIS A083342) appears in the summatory function of the number of (not necessarily distinct) prime factors 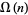 ,
,
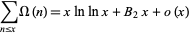 |
(15) |
(Hardy and Wright 1979, p. 355), where 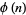 is the totient function and
is the totient function and 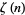 is the Riemann zeta function.
is the Riemann zeta function.
Another related constant is
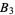 |
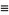 |
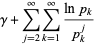 |
(16) |
 |
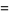 |
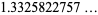 |
(17) |
(OEIS A083343; Rosser and Schoenfeld 1962, Montgomery 1971, Finch 2003), which appears in another equivalent form of the Mertens theorem
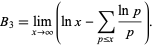 |
(18) |
REFERENCES:
Bach, E. and Shallit, J. Algorithmic Number Theory, Vol. 1: Efficient Algorithms. Cambridge, MA: MIT Press, 1996.
Ellison, W. J. and Ellison, F. Prime Numbers. New York: Wiley, 1985.
Finch, S. R. "Meissel-Mertens Constants." §2.2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 94-98, 2003.
Flajolet, P. and Vardi, I. "Zeta Function Expansions of Classical Constants." Unpublished manuscript. 1996. http://algo.inria.fr/flajolet/Publications/landau.ps.
Gourdon, X. and Sebah, P. "Some Constants from Number Theory." http://numbers.computation.free.fr/Constants/Miscellaneous/constantsNumTheory.html.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Wright, E. M. "Mertens's Theorem." §22.8 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Oxford University Press, pp. 351-353 and 355, 1979.
Ingham, A. E. The Distribution of Prime Numbers. London: Cambridge University Press, pp. 22-24, 1990.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1998.
Landau, E. Handbuch der Lehre von der Verteilung der Primzahlen, 3rd ed. New York: Chelsea, pp. 100-102, 1974.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 24, 1983.
Lindqvist, P. and Peetre, J. "On the Remainder in a Series of Mertens." Expos. Math. 15, 467-478, 1997.
Mertens, F. J. für Math. 78, 46-62, 1874.
Michon, G. P. "Final Answers: Numerical Constants." http://home.att.net/~numericana/answer/constants.htm#mertens.
Montgomery, H. L. Topics in Multiplicative Number Theory. New York: Springer-Verlag, 1971.
Rosser, J. B. and Schoenfeld, L. "Approximate Formulas for Some Functions of Prime Numbers." Ill. J. Math. 6, 64-94, 1962.
Schroeder, M. R. Number Theory in Science and Communication, with Applications in Cryptography, Physics, Digital Information, Computing, and Self-Similarity, 3rd ed. New York: Springer-Verlag, 1997.
Sloane, N. J. A. Sequences A077761, A083342, and A083343 in "The On-Line Encyclopedia of Integer Sequences."
Tenenbaum, G. and Mendes-France, M. The Prime Numbers and Their Distribution. Providence, RI: Amer. Math. Soc., p. 22, 2000.
Titchmarsh, E. C. The Theory of the Riemann Zeta Function, 2nd ed. New York: Clarendon Press, 1987.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
قسم الشؤون الفكرية والثقافية يجري اختبارات مسابقة حفظ دعاء أهل الثغور
|
|
|