Happy Number

Let the sum of the squares of the digits of a positive integer 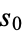 be represented by 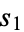. In a similar way, let the sum of the squares of the digits of  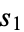be represented by 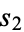, and so on.

Iterating this sum-of-squared-digits map always eventually reaches one of the 10 numbers 0, 1, 4, 16, 20, 37, 42, 58, 89, or 145 (OEIS A039943; Porges 1945).

If 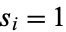 for some 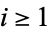, then the original integer  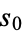is said to be happy. For example, starting with 7 gives the sequence 7, 49, 97, 130, 10, 1, so 7 is a happy number.

The first few happy numbers are 1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, ... (OEIS A007770). These are also the numbers whose 2-recurring digital invariant sequences have period 1. The numbers of iterations required for these to reach 1 are 0, 5, 1, 2, 4, 3, 3, 2, 3, 4, 4, 2, 5, ... (OEIS A090425).

The numbers of happy numbers less than or equal to 1, 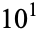, , 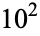... are given by 1, 3, 20, 143, 1442, 14377, 143071, ... (OEIS A068571).

The first few consecutive happy numbers 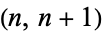 have 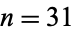, 129, 192, 262, 301, 319, 367, 391, ... (OEIS A035502). Similarly, the first few happy triplets start with 1880, 4780, 4870, 7480, 7839, ... (OEIS A072494).

The first few happy primes are 7, 13, 19, 23, 31, 79, 97, 103, 109, 139, ... (OEIS A035497).

Once it is known whether a number is happy (or not), then any number in the sequence 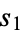, , 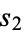, 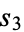... will also be happy (or not). A number that is not happy is called unhappy. Unhappy numbers have eventually periodic sequences of  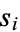which never reach 1.

Any permutation of the digits of an unhappy or happy number must also be unhappy or happy. This follows from the fact that addition is commutative.

REFERENCES:

Dudeney, H. E. Problem 143 in 536 Puzzles & Curious Problems. New York: Scribner, pp. 43 and 258-259, 1967.

Guy, R. K. "Happy Numbers." §E34 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 234-235, 1994.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 163-165, 1979.

Porges, A. "A Set of Eight Numbers." Amer. Math. Monthly 52, 379-382, 1945.

Rivera, C. "Problems & Puzzles: Puzzle 021-Happy Primes." https://www.primepuzzles.net/puzzles/puzz_021.htm.

Schneider, W. "MATHEWS: Happy Numbers." https://www.wschnei.de/digit-related-numbers/happy-numbers.html.

Schwartzman, S. The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. Washington, DC: Math. Assoc. Amer., 1994.

Sloane, N. J. A. Sequences A007770, A035497, A035502, A039943, A068571, A072494, and A090425 in "The On-Line Encyclopedia of Integer Sequences."