


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-11-2020
Date: 22-11-2019
Date: 11-3-2020
|
A set of positive integers is double-free if, for any integer  , the set
, the set 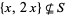 (or equivalently,
(or equivalently, 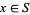 implies
implies 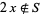 ). For example, of the subsets of
). For example, of the subsets of 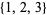 , the sets
, the sets 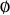 ,
, 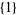 ,
, 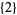 ,
, 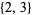 ,
, 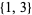 , and
, and 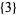 are double-free, while
are double-free, while 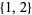 and
and 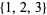 are not.
are not.
The number 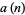 of double-free subsets of
of double-free subsets of 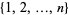 can be computed using
can be computed using 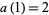 and the recurrence relation
and the recurrence relation
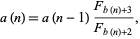 |
(1) |
where 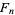 is a Fibonacci number, 1, 1, 2, 3, 5, 8, ... (OEIS A000045), and
is a Fibonacci number, 1, 1, 2, 3, 5, 8, ... (OEIS A000045), and 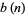 is the binary carry sequence giving the number of trailing 0s in the binary representation of
is the binary carry sequence giving the number of trailing 0s in the binary representation of 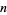 . For
. For 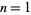 , 2, ...,
, 2, ..., 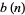 is given by 0, 1, 0, 2, 0, 1, 3, 0, 1, ... (OEIS A007814), while the corresponding
is given by 0, 1, 0, 2, 0, 1, 3, 0, 1, ... (OEIS A007814), while the corresponding 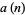 are 2, 3, 6, 10, 20, 30, 60, 96, 192, ... (OEIS A050291).
are 2, 3, 6, 10, 20, 30, 60, 96, 192, ... (OEIS A050291).
Define
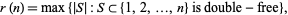 |
(2) |
where 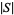 is the cardinal number of (number of members in)
is the cardinal number of (number of members in) 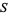 . Then for
. Then for 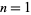 , 2, ...,
, 2, ..., 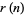 is given by 1, 1, 2, 3, 4, 4, 5, 5, 6, 6, 7, 8, 9, 9, 10, ... (OEIS A050292). An explicit formula for
is given by 1, 1, 2, 3, 4, 4, 5, 5, 6, 6, 7, 8, 9, 9, 10, ... (OEIS A050292). An explicit formula for 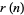 is given by
is given by
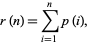 |
(3) |
where
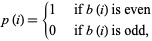 |
(4) |
if the characteristic function of 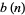 (defined above), and the first few values of
(defined above), and the first few values of 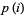 are 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, ... (OEIS A035263). A simple recurrence relation for
are 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, ... (OEIS A035263). A simple recurrence relation for 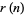 is given by
is given by
![f(n)=[1/2n]+f(|_1/4n_|)](https://mathworld.wolfram.com/images/equations/Double-FreeSet/NumberedEquation5.gif) |
(5) |
with 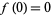 (Wang 1989), where
(Wang 1989), where 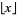 is the floor function and
is the floor function and ![[x]](https://mathworld.wolfram.com/images/equations/Double-FreeSet/Inline33.gif) is the ceiling function. An asymptotic formula for
is the ceiling function. An asymptotic formula for 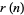 is given by
is given by
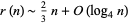 |
(6) |
(Wang 1989).
REFERENCES:
Finch, S. R. "Triple-Free Set Constants." §2.26 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 183-185, 2003.
Sloane, N. J. A. Sequences A000045/M0692, A007814, A035263, A050291 and A050292 in "The On-Line Encyclopedia of Integer Sequences."
Wang, E. T. H. "On Double-Free Sets of Integers." Ars Combin. 28, 97-100, 1989.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
جامعة الفلوجة: حفل تخرج طلبة الجامعات يهدف إلى جمع الطلبة تحت خيمة العراق الموحد
|
|
|