


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-4-2020
Date: 21-1-2021
Date: 18-2-2020
|
A prime which does not divide the class number 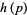 of the cyclotomic field obtained by adjoining a primitive pth root of unity to the field of rationals. A prime
of the cyclotomic field obtained by adjoining a primitive pth root of unity to the field of rationals. A prime 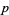 is regular iff
is regular iff 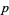 does not divide the numerators of the Bernoulli numbers
does not divide the numerators of the Bernoulli numbers 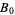 ,
, 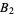 , ...,
, ..., 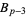 . A prime which is not regular is said to be an irregular prime.
. A prime which is not regular is said to be an irregular prime.
In 1915, Jensen proved that there are infinitely many irregular primes. It has not yet been proven that there are an infinite number of regular primes (Guy 1994, p. 145). Of the 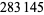 primes
primes 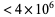 ,
, 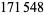 (or 60.59%) are regular (the conjectured fraction is
(or 60.59%) are regular (the conjectured fraction is 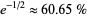 ). The first few are 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 43, 47, ... (OEIS A007703).
). The first few are 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 43, 47, ... (OEIS A007703).
REFERENCES:
Buhler, J.; Crandall, R. Ernvall, R.; and Metsankyla, T. "Irregular Primes and Cyclotomic Invariants to Four Million." Math. Comput. 61, 151-153, 1993.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 145, 1994.
Ribenboim, P. "Regular Primes." §5.1 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 323-329, 1996.
Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, p. 153, 1993.
Sloane, N. J. A. Sequence A007703/M2411 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|