


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-5-2020
Date: 10-1-2021
Date: 17-11-2019
|
In August 2002, M. Agrawal and colleagues announced a deterministic algorithm for determining if a number is prime that runs in polynomial time (Agrawal et al. 2004). While this had long been believed possible (Wagon 1991), no one had previously been able to produce an explicit polynomial time deterministic algorithm (although probabilistic algorithms were known that seem to run in polynomial time). This test is now known as the Agrawal-Kayal-Saxena primality test, cyclotomic AKS test, or AKS primality test.
Commenting on the impact of this discovery, P. Leyland noted, "One reason for the excitement within the mathematical community is not only does this algorithm settle a long-standing problem, it also does so in a brilliantly simple manner. Everyone is now wondering what else has been similarly overlooked" (quoted by Crandall and Papadopoulos 2003).
The complexity of the original algorithm of Agrawal et al. (2004) was 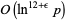 , but has since been considerably reduced to
, but has since been considerably reduced to 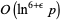 for general integers (Lenstra and Pomerance 2003), or
for general integers (Lenstra and Pomerance 2003), or 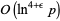 for certain integers or with an infinitesimal chance that the algorithm might return an ambiguous result (Crandall and Papadopoulos 2003).
for certain integers or with an infinitesimal chance that the algorithm might return an ambiguous result (Crandall and Papadopoulos 2003).
REFERENCES:
Agrawal, M.; Kayal, N.; and Saxena, N. "Primes is in P." Ann. Math. 160, 781-793, 2004. https://www.cse.iitk.ac.in/users/manindra/algebra/primality_v6.pdf.
Bailey, D. H.; Borwein, J. M.; Calkin, N. J.; Girgensohn, R.; Luke, D. R.; and Moll, V. H. Experimental Mathematics in Action. Wellesley, MA: A K Peters, p. 58, 2007.
Bernstein, D. J. "An Exposition of the Agrawal-Kayal-Saxena Primality-Proving Theorem." Preprint. 2002. https://cr.yp.to/papers/aks.ps.
Bernstein D. J. "Proving Primality After Agrawal-Kayal-Saxena." Preprint. 25 Jan 2003. https://modular.ucsd.edu/edu/Spring2004/129/references/primes/Bernstein-Proving%20primality%20after%20Agrawal-Kayal-Saxena.pdf.
Bernstein D. J. "Proving Primality in Essentially Quartic Expected Time." Preprint. 28 Jan 2003.
Berrizbeitia, P. "Sharpening 'Primes Is in P' for a Large Family of Numbers." Preprint. 20 Nov 2002.
Borwein, J. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, p. 6, 1987.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Bornemann, F. "PRIMES Is in P: A Breakthrough for 'Everyman.' " Notices Amer. Math. Soc. 50, 545-552, 2003.
Clark, E. "Polynomial Time Primality Test." sci.math newsgroup posting. 6 Aug 2002.
Crandall, R. and Papadopoulos, J. "On the Implementation of AKS-Class Primality Tests." 18 Mar 2003. https://developer.apple.com/hardware/ve/pdf/aks3.pdf.
Crandall, R. and Pomerance, C. Prime Numbers: A Computational Perspective, 2nd ed. New York: Springer-Verlag, 2005.
Germundsson, R.; Lichtblau, D.; and Terr, D. "The Agarwal-Kayal-Saxena Primality Test." https://library.wolfram.com/infocenter/Demos/4956/.
Granville, A. "It Is Easy to Determine Whether a Given Integer Is Prime." Bull. Amer. Math. Soc. 42, 3-38, 2005.
Indian Institute of Technology. "PRIMES is in P." https://www.cse.iitk.ac.in/news/primality.html
Kayal, N. and Saxena, N. "Towards a Deterministic Polynomial-Time Test." Technical Report. Kanpur, India: Indian Institute of Technology, 2002. https://www.cse.iitk.ac.in/research/btp2002/primality.html.
Lenstra H. W. Jr. "Primality Testing with Cyclotomic Rings." Preprint. 14 Aug 2002.
Lenstra H. W. Jr. and Pomerance C. "Primality Testing with Gaussian Periods." Manuscript. March 2003.
Pomerance, C. "The Cyclotomic Ring Test of Agrawal, Kayal, and Saxena." Preprint. 2002.
Pomerance, C. "RE: New Polynomial Time Primality Test?" 7 Aug 2002a. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0208&L=NMBRTHRY&F=&S=&P=956.
Pomerance, C. "A New Primal Screen." FOCUS: Newsletter of the Math. Assoc. Amer. 22, No. 8, 4-5, 2002.
Robinson, S. "New Method Said to Solve Key Problem in Math." New York Times, p. A16, August 8, 2002.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 15-17, 1991.
Weisstein, E. W. "Primality Testing Is Easy." MathWorld Headline News, Aug. 7, 2002. https://mathworld.wolfram.com/news/2002-08-07/primetest/.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|