


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 8-9-2020
Date: 23-11-2020
Date: 17-8-2020
|
Limiting magnitude
The amount of energy collected by any aperture is proportional to its area and, therefore, to the square of its diameter. In the case of the eye, the sensitive area responds to the energy which is accepted by the pupil and, accordingly, there is a limit to the strength of radiation that can be detected. For starlight, the limit of unaided eye detection is set at about sixth magnitude. By using a telescope, with its greatly increased aperture over the pupil of the eye, it should be possible to record stars which are much fainter than sixth magnitude.
The brightness of the sixth magnitude star corresponds to the arrival of a certain amount of energy per unit area per unit time. Thus, if the star of naked eye brightness Be is viewed by a telescope, its apparent brightness, Bt , will be given by
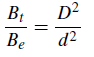 (1)
(1)
where D and d are the diameters of the telescope and eye pupil respectively, provided that the telescope is used with a sufficient magnification so that all the collected light enters the eye. If me and mt correspond to the magnitude of a star as seen by the naked eye and by the telescope, respectively, the apparent difference in magnitude can be obtained by using Pogson’s equation . Thus,
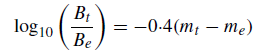
and, by using equation (17.11), this becomes
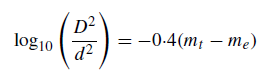
which may be re-written as
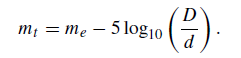 (2)
(2)
By letting mt correspond to the faintest star that can be detected by the telescope–eye combination (i.e. mt = 6), then the value obtained for me via equation (2), corresponds to the original magnitude of the star. This value is known as the limiting magnitude, mlim, of the telescope and, if a typical value of d = 8·0 mm is used, it can be expressed as
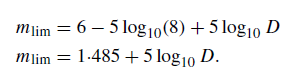 (3)
(3)
Thus, for a telescope of 500 mm, the theoretical limiting magnitude is approximately 15·0. In this discussion it has been assumed that the transmission efficiency of the telescope is perfect. A typical figure for the efficiency is about 0·65 (including losses in the eyepiece) and, to allow for this, equation (1) should be corrected so that it becomes
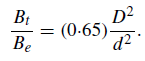
Consequently, equation (2) should be corrected to
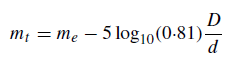
and, by rounding off the figures, the equation expressing the limiting magnitude of the telescope may be written as
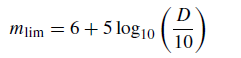 (4)
(4)
where D is expressed in mm. Thus, in practice, the limiting magnitude for a 500 mm telescope is likely to be about 14·5. Half a magnitude has been ‘lost’ due to the telescope’s imperfect transmission. Equation (4) is again not a hard and fast law, however, as each telescope must be treated individually and also the limiting magnitude will depend on the observer to some extent.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|