The telescope and the collected energy: Stellar brightness
 

When any object such as a star can be considered as a point source, to all intents and purposes its telescope image can also be considered as a point, no matter how large a telescope is used. All the collected radiation is concentrated into this image. The larger the telescope, the greater is the amount of collected radiation for detection. Thus, the apparent brightness of a star is increased according to the collection area or the square of the diameter of the collector.
In allowing detection and measurement of faint stars, the role of the telescope may be summarized as being that of a flux collector.
Although stellar brightness measurements are usually expressed on a magnitude scale, they result from observations of the amount of energy collected by a telescope within some defined spectral interval over a certain integration time. A stellar brightness may be put on absolute scale and be described in terms of the flux, , or the energy received per unit area per unit wavelength interval per unit time. A measure of the star’s brightness might be expressed in units of W m⁻² ˚A⁻¹. Estimation of the strength of any recorded signal and determination of the signal-to-noise ratio of any measurement is normally performed in terms of the number of photons arriving at the detector. In the first instance, the calculations involve determination of the number of photons passing through the telescope collector and this can be done by remembering that the energy associated with each photon is given by E = hν or E = hc/λ . Thus, the number of photons at the telescope aperture may be written as
(1)
where λ₁ and λ₂ are the cut-on and cut-off points for the spectral range of the measurements and Δt is the integration time of the measurement.

If the stellar spectrum is relatively flat over the detected wavelength interval and if it is assumed that the photon energy is constant over this interval, then we may write
(2)
where Δλ is the spectral interval for the measurements.
The arrival of photons at the telescope is a statistical process. When the arriving flux is low, fluctuations are clearly seen in any recorded signal as a result and any measurements are said to suffer from photon shot noise. If no other sources of noise are present, the uncertainty of any measurement is given by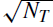. Hence, any record and its ‘error’ may be expressed as NT ±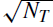. In this circumstance, the signal-to-noise (S/N) ratio of the observation is given by
(3)
Although the light gathering power of a telescope depends on its collection area and hence on D², equation (3) shows that the signal-to-noise ratio of basic brightness measurements only increases according to D. It may also be noted that the S/N ratio improves according to the square root of the observational time illustrating a law of diminishing returns according to the time spent making any measurement. As will be seen later, in the real situation, the signal strengths depend on the photon detection rate, after taking into account the transmittance of the telescope and its subsidiary instrumentation and the efficiency of the detector. However, these additional factors do not alter the conclusions coming from equation (3).
In passing, it may also be mentioned that under some circumstances of detection of faint objects, the effectiveness of a telescope may not be proportional to D². For example, when faint stars are being detected photoelectrically against a background night sky which is also emitting light (no sky is perfectly black), measurements of the night sky brightness need to be made also so that this background signal can be subtracted and allowed for. In this circumstance, where observations are required of the star plus sky background and then sky background alone, the effectiveness of the telescope is then only proportional to D.