Kepler’s third law
 

In the third law, Kepler obtained a relationship between the sizes of planetary orbits and the periods of revolution. Now it happens that the semi-major axis of a planetary orbit is the average size of the radius vector, or the mean distance, so that an alternative form of the third law is to say that the cube of the mean distance of a planet is proportional to the square of its period of revolution.
Hence, if a₁ and T₁ refer to the semi-major axis and sidereal period of a planet P₁ moving about the Sun,
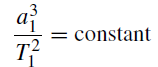(1)
the constant being the same for any of the planetary orbits. If a₂, a₃, etc and T₂, T₃, etc refer to the semi-major axes and sidereal periods of the other planets P₂, P₃, etc moving about the Sun, then

The most convenient form of the constant is obtained by taking the planet to be the Earth in relation (1), expressing the distance in units of the Earth’s semi-major axis and the time in years.
Then, for the Earth, a₁ = 1, T₁ = 1 and so the constant becomes unity. For any other planet, consequently,
a³ = T² (2)
showing that if we measure the sidereal period, T , of the planet, we can obtain its mean distance, a, from relation (2).

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الدينية يوزع أكثر من ألفي وجبة طعام للمعزين في ذكرى عاشوراء بنينوى

قسم الشؤون الطبية يواصل تقديم خدماته الصحية لزائري عاشوراء

جموع المعزين تحيي مراسم يوم العاشر من شهر المحرم عند المرقدين الطاهرين

قسم العلاقات يطلق محطات فتية الكفيل الثقافية في محافظة نينوى

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

اختبار الانفجار الهائل

الكوسمولوجيا وأشكال كالابي - ياو

التخمينات الكوسمولوجيا والنظرية النهائية

النموذج القياسي للكوسمولوجيا، أو علم الكون

تأملات في علم الكون

المذنبات

الصعود إلى الفضاء

اختلاف الليل والنهار

تصنيع الصاروخ و اطلاقة

الكويكبات والمذنبات

صورة الحجر الأزتكي (فهم وإدراك الحضارة الآزيتية )

الهالات المجرية