Kepler’s second law
 

This law states that the rate of description of area by the planet’s radius vector is a constant. Let us suppose that in figure 13.3, the planet’s positions at times t₁, t₂, t₃ and t4 are P₁, P₂, P₃ and P₄. Then between times t₁ and t₂ its radius vector has swept out the area bounded by the radius vectors SP₁, SP₂ and the arc P₁P₂. Similarly, the area swept out by the radius vector in the time interval (t₄ − t₃) is the area SP₃P₄.
Then Kepler’s law states that
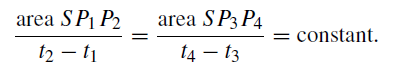(1)
If t₂ − t₁ = t₄ − t₃, then the area SP₁P₂ = area SP₃P₄.
In particular, if the area is the area of the ellipse itself, the radius vector will be back to its original position and Kepler’s second law, therefore, implies that the planet’s period of revolution is constant. Let us suppose the time interval (t₂ − t₁) to be very small and equal to interval (t₄ − t₃). Position P₂ will be very close to P₁, just as P₄ will be close to P₃. The area SP₁P₂ is then approximately the area of ΔSP₁P₂ or
1/2 SP₁ × SP₂ × sin P₁SP₂.

If ∠P1SP2 is expressed in radians, we may write
sin P₁SP₂ = ∠P₁SP₂ = θ₁
since ∠P₁SP₂ is very small. Also,
SP₁ ≈ SP₂ = r₁ say
so that the area SP₁P₂ is given by

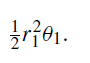
Similarly, area SP₃P₄ is given by

where SP₃ = r₂ and ∠P₃SP₄ = θ₂. Let t₄ − t₃ = t₂ − t₁ = t. Then by equation (1),

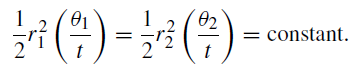
But θ/t is the angular velocity, ω, in the limit when t tends to zero. Hence,
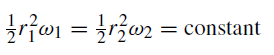(2)
is the mathematical expression of Kepler’s second law.
In order that this law is obeyed, the planet has to move fastest when its radius vector is shortest, at perihelion, and slowest when it is at aphelion.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

اختبار الانفجار الهائل

الكوسمولوجيا وأشكال كالابي - ياو

التخمينات الكوسمولوجيا والنظرية النهائية

النموذج القياسي للكوسمولوجيا، أو علم الكون

تأملات في علم الكون

المذنبات

الصعود إلى الفضاء

اختلاف الليل والنهار

تصنيع الصاروخ و اطلاقة

الكويكبات والمذنبات

صورة الحجر الأزتكي (فهم وإدراك الحضارة الآزيتية )

الهالات المجرية