Stellar parallax: Stellar parallactic movements
 

The direction of a star as seen from the Earth is not the same as the direction when viewed by a hypothetical observer at the Sun’s centre. As the Earth moves in its yearly orbit round the Sun, the geocentric direction (the star’s position on a geocentric celestial sphere) changes and traces out what is termed the parallactic ellipse. Thus, in figure 1, the star X at a distance d kilometres is seen from the Earth at E₁ to lie in the direction E₁X₁ relative to the heliocentric direction SX'. Six months later, the Earth is now at the point E₂ in its orbit and the geocentric direction of the star is E₂X₂.
The concepts used in stellar parallax are analogous to those used in geocentric parallax. Thus, if we looked upon the Earth’s orbital radius a as the base-line, we can define the star’s parallax as P, given by

.........(1)

Because stellar distances are so great compared with the Earth’s orbital radius, we can assume that the Earth’s orbit to be circular. Angle P is small so that we can write equation (1) as

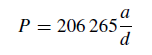
where P is in seconds of arc.
Again, if we draw E1Y parallel to SX in figure 1. and let ∠Y E₁X = ∠E₁XS = p, we have, from ΔE₁XS,

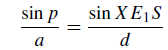
or

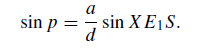
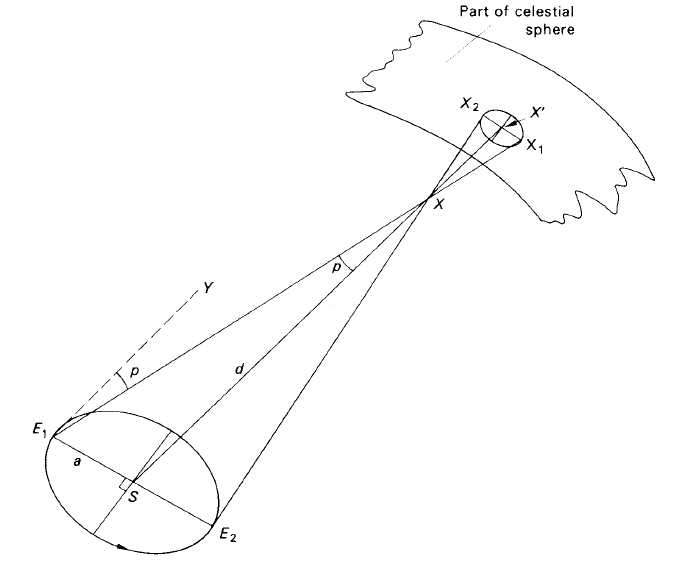
Figure 1. The parallactic ellipse (the size is exaggerated for clarity).
 

Using equation (1) and letting ∠XE₁S = θ, we obtain
sin p = sin P sin θ
or
p = P sin θ (2)
since both p and P are small angles.
Thus, the star is displaced towards the Sun along the great circle through the star’s heliocentric position and the Sun by an amount p, given by equation (2), where P is the star’s parallax and θ is the angle between the Sun’s direction and the star’s. Whereas P remains constant, p and θ vary because of the Earth’s movement in its orbit about the Sun.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

اختبار الانفجار الهائل

الكوسمولوجيا وأشكال كالابي - ياو

التخمينات الكوسمولوجيا والنظرية النهائية

النموذج القياسي للكوسمولوجيا، أو علم الكون

تأملات في علم الكون

المذنبات

الصعود إلى الفضاء

اختلاف الليل والنهار

تصنيع الصاروخ و اطلاقة

الكويكبات والمذنبات

صورة الحجر الأزتكي (فهم وإدراك الحضارة الآزيتية )

الهالات المجرية