Swinnerton-Dyer Conjecture

In the early 1960s, B. Birch and H. P. F. Swinnerton-Dyer conjectured that if a given elliptic curve has an infinite number of solutions, then the associated 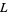-series has value 0 at a certain fixed point. In 1976, Coates and Wiles showed that elliptic curves with complex multiplication having an infinite number of solutions have 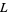-series which are zero at the relevant fixed point (Coates-Wiles theorem), but they were unable to prove the converse. V. Kolyvagin extended this result to modular curves.

REFERENCES:

Birch, B. and Swinnerton-Dyer, H. "Notes on Elliptic Curves. II." J. reine angew. Math. 218, 79-108, 1965.

Cipra, B. "Fermat Prover Points to Next Challenges." Science 271, 1668-1669, 1996.

Clay Mathematics Institute. "The Birch and Swinnerton-Dyer Conjecture." https://www.claymath.org/millennium/Birch_and_Swinnerton-Dyer_Conjecture/.

Ireland, K. and Rosen, M. "New Results on the Birch-Swinnerton-Dyer Conjecture." §20.5 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 353-357, 1990.

Mazur, B. and Stevens, G. (Eds.). p-Adic Monodromy and the Birch and Swinnerton-Dyer Conjecture. Providence, RI: Amer. Math. Soc., 1994.

Wiles, A. "The Birch and Swinnerton-Dyer Conjecture." https://www.claymath.org/millennium/Birch_and_Swinnerton-Dyer_Conjecture/BSD.pdf.