
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-9-2020
Date: 7-10-2020
Date: 5-2-2016
|
Lucas's theorem states that if 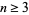 be a squarefree integer and
be a squarefree integer and 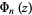 a cyclotomic polynomial, then
a cyclotomic polynomial, then
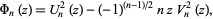 |
(1) |
where 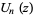 and
and 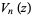 are integer polynomials of degree
are integer polynomials of degree 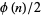 and
and 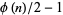 , respectively. This identity can be expressed as
, respectively. This identity can be expressed as
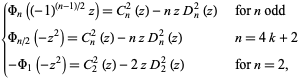 |
(2) |
with 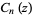 and
and 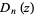 symmetric polynomials. The following table gives the first few
symmetric polynomials. The following table gives the first few 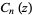 and
and 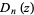 s (Riesel 1994, pp. 443-456).
s (Riesel 1994, pp. 443-456).
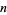 |
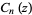 |
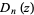 |
| 2 | 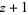 |
1 |
| 3 | 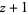 |
1 |
| 5 | 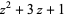 |
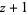 |
| 6 | 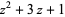 |
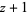 |
| 7 | 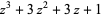 |
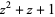 |
| 10 | 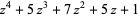 |
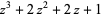 |
REFERENCES:
Brent, R. P. "On Computing Factors of Cyclotomic Polynomials." Math. Comput. 61, 131-149, 1993.
Kraitchik, M. Recherches sue la théorie des nombres, tome I. Paris: Gauthier-Villars, pp. 126-128, 1924.
Riesel, H. "Lucas's Formula for Cyclotomic Polynomials." In tables at end of Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 443-456, 1994.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|