


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-8-2020
Date: 18-10-2020
Date: 6-12-2020
|
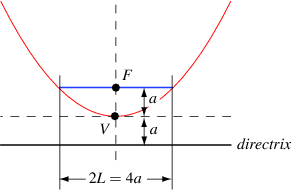
Just as the ratio of the arc length of a semicircle to its radius is always  , the ratio
, the ratio  of the arc length of the parabolic segment formed by the latus rectum of any parabola to its semilatus rectum (and focal parameter) is a universal constant
of the arc length of the parabolic segment formed by the latus rectum of any parabola to its semilatus rectum (and focal parameter) is a universal constant
 |
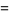 |
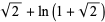 |
(1) |
 |
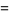 |
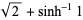 |
(2) |
 |
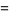 |
 |
(3) |
 |
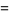 |
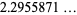 |
(4) |
(OEIS A103710). This can be seen from the equation of the arc length of a parabolic segment
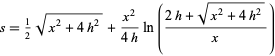 |
(5) |
by taking 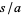 and plugging in
and plugging in 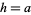 and
and 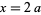 .
.
The other conic sections, namely the ellipse and hyperbola, do not have such universal constants because the analogous ratios for them depend on their eccentricities. In other words, all circles are similar and all parabolas are similar, but the same is not true for ellipses or hyperbolas (Ogilvy 1990, p. 84).
The area of the surface generated by revolving 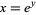 for
for ![y in (-infty,0]](http://mathworld.wolfram.com/images/equations/UniversalParabolicConstant/Inline19.gif) about the
about the 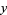 -axis is given by
-axis is given by
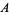 |
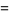 |
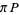 |
(6) |
 |
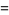 |
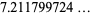 |
(7) |
(Love 1950, p. 288; OEIS A103713) and the area of the surface generated by revolving 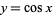 for
for ![x in [-pi/2,pi/2]](http://mathworld.wolfram.com/images/equations/UniversalParabolicConstant/Inline28.gif) about the
about the  -axis is
-axis is
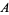 |
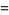 |
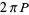 |
(8) |
 |
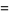 |
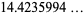 |
(9) |
(Love 1950, p. 288; OEIS A103714).
The expected distance from a randomly selected point in the unit square to its center (square point picking) is
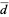 |
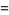 |
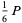 |
(10) |
 |
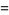 |
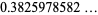 |
(11) |
(Finch 2003, p. 479; OEIS A103712).
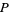 is an irrational number. It is also a transcendental number, as can be seen as follows. If
is an irrational number. It is also a transcendental number, as can be seen as follows. If 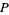 were algebraic, then
were algebraic, then 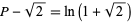 would also be algebraic. But then, by the Lindemann-Weierstrass theorem,
would also be algebraic. But then, by the Lindemann-Weierstrass theorem, 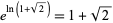 would be transcendental, which is a contradiction.
would be transcendental, which is a contradiction.
REFERENCES:
Finch, S. R. Mathematical Constants. Cambridge, England: Cambridge University Press, p. 479, 2003.
Love, C. E. Differential and Integral Calculus, 4th ed. New York: Macmillan, 1950.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, 1990.
Sloane, N. J. A. Sequences A103710, A103711, A103712, A103713, and A103714 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
العتبة الحسينية تطلق فعاليات المخيم القرآني الثالث في جامعة البصرة
|
|
|