المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Gaussian Triangle Picking |
 761
 04:54 مساءً
date: 8-2-2020 |
Author : Eisenberg, B. and Sullivan, R. 
Book or Source : "Random Triangles n Dimensions." Amer. Math. Monthly 103 
Page and Part : ...|
Read More
Date: 14-1-2020
935
Date: 31-1-2020
2132
Date: 9-1-2020
849
|
Finch (2010) gives an overview of known results for random Gaussian triangles.
Let the vertices of a triangle in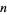 
dimensions be normal (normal) variates. The probability that a Gaussian triangle in 
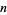dimensions is obtuse is
 |
 |
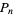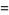![(3Gamma(n))/([Gamma(1/2n)]^2)int_0^(1/3)(x^((n-2)/2))/((1+x)^n)dx](http://mathworld.wolfram.com/images/equations/GaussianTrianglePicking/Inline5.gif) |
(1) |
 |
 |
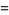![(3Gamma(n))/([Gamma(1/2n)]^22^(n-1))int_0^(pi/3)sin^(n-1)thetadtheta](http://mathworld.wolfram.com/images/equations/GaussianTrianglePicking/Inline8.gif) |
(2) |
 |
 |
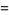![(6Gamma(n)_2F_1(1/2n,n;1+1/2n;-1/3))/(3^(n/2)n[Gamma(1/2n)]^2)](http://mathworld.wolfram.com/images/equations/GaussianTrianglePicking/Inline11.gif) |
(3) |
 |
 |
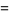![(3B(-1/3;1/2n,1-n)Gamma(n))/([Gamma(1/2n)]^2)](http://mathworld.wolfram.com/images/equations/GaussianTrianglePicking/Inline14.gif) |
(4) |
 |
 |
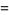![(3B(3/4;1/2n,1/2)Gamma(n))/([Gamma(1/2n)]^2),](http://mathworld.wolfram.com/images/equations/GaussianTrianglePicking/Inline17.gif) |
(5) |
where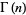 
is the gamma function, 
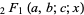is the hypergeometric function, and 
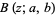is an incomplete beta function.
For even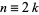 
,
 |
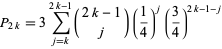(6) |
(Eisenberg and Sullivan 1996).
The first few cases are explicitly
 |
 |
 |
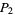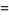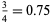(7) |
 |
 |
 |
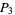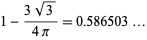(8) |
 |
 |
 |
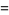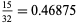(9) |
 |
 |
 |
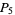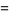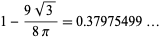(10) |
(OEIS A102519 and A102520). The even cases are therefore 3/4, 15/32, 159/512, 867/4096, ... (OEIS A102556 and A102557) and the odd cases are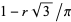 
, where 
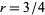, 9/8, 27/20, 837/560, ... (OEIS A102558 and A102559).
REFERENCES:
Eisenberg, B. and Sullivan, R. "Random Triangles 
Dimensions." Amer. Math. Monthly 103, 308-318, 1996.
Finch, S. "Random Triangles." http://algo.inria.fr/csolve/rtg.pdf. Jan. 21, 2010.
Sloane, N. J. A. Sequences A102519, A102520, A102556, A102557, A102558, and A102559 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|
