


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-5-2020
Date: 28-7-2020
Date: 8-9-2020
|
A function is said to be modular (or "elliptic modular") if it satisfies:
1. 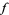 is meromorphic in the upper half-plane
is meromorphic in the upper half-plane 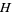 ,
,
2. 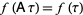 for every matrix
for every matrix 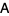 in the modular group Gamma,
in the modular group Gamma,
3. The Laurent series of 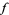 has the form
has the form
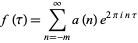 |
(Apostol 1997, p. 34). Every rational function of Klein's absolute invariant 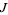 is a modular function, and every modular function can be expressed as a rational function of
is a modular function, and every modular function can be expressed as a rational function of 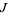 (Apostol 1997, p. 40). Modular functions are special cases of modular forms, but not vice versa.
(Apostol 1997, p. 40). Modular functions are special cases of modular forms, but not vice versa.
An important property of modular functions is that if 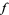 is modular and not identically 0, then the number of zeros of
is modular and not identically 0, then the number of zeros of 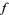 is equal to the number of poles of
is equal to the number of poles of 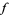 in the closure of the fundamental region
in the closure of the fundamental region 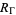 (Apostol 1997, p. 34).
(Apostol 1997, p. 34).
REFERENCES:
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, 1997.
Askey, R. "Ramanujan and Hypergeometric and Basic Hypergeometric Series." In Ramanujan International Symposium on Analysis: Proceedings of the Ramanujan Birth Centenary Year International Symposium held in Pune, December 26-28, 1987 (Ed. N. K. Thakare, K. C. Sharma and T. T. Raghunathan). New Delhi: Macmillan of India, pp. 1-83, 1989.
Borwein, J. M. and Borwein, P. B. "Elliptic Modular Functions." §4.3 in Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, pp. 112-116, 1987.
Rademacher, H. "Zur Theorie der Modulfunktionen." J. reine angew. Math. 167, 312-336, 1932.
Rankin, R. A. Modular Forms and Functions. Cambridge, England: Cambridge University Press, 1977.
Schoeneberg, B. Elliptic Modular Functions: An Introduction. Berlin: New York: Springer-Verlag, 1974.
Weisstein, E. W. "Books about Modular Functions." http://www.ericweisstein.com/encyclopedias/books/ModularFunctions.html.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|