A simple continued fraction is a special case of a generalized continued fraction for which the partial numerators are equal to unity, i.e., 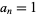 for all 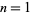, 2, .... A simple continued fraction is therefore an expression of the form

(1)

When used without qualification, the term "continued fraction" is often used to mean "simple continued fraction" or, more specifically, regular (i.e., a simple continued fraction whose partial denominators 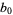, , 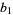... are positive integer; Rockett and Szüsz 1992, p. 3). Care must therefore be taken to identify the intended meaning based on the context in which such terminology is encountered.

A simple continued fraction can be written in a compact abbreviated notation as

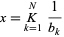(2)

or

(3)

where 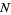 may be finite (for a finite continued fraction) or  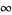(for an infinite continued fraction). In contexts where only simple continued fractions are considered, the partial denominators are often denoted  instead of  (e.g., Rockett and Szüsz 1992, p. 3), a practice which unfortunately conflicts with the common notation for generalized continued fractions in which 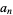 denotes a partial numerator.

Further care is needed when encountering bracket notation for simple continued fractions since some authors replace the semicolon with a normal comma and begin indexing the terms at 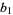 instead of 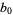, writing  instead of  or , causing ambiguity in the meaning of the initial term and resulting in the parity of certain fundamental results in continued fraction theory to be reversed. To complicate matters a bit further, Gaussian brackets use the notation  to denote a different (but closely related) combination of partial denominators.

The terms 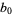 through  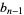of the simple continued fraction of a number  can be computed in the Wolfram Language using the command ContinuedFraction[x, n]. Similarly, the 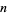 convergent of simple continued fraction with partial denominators  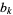can be continued using ContinuedFractionK[a[k], {" src="https://mathworld.wolfram.com/images/equations/SimpleContinuedFraction/Inline21.gif" style="height:15px; width:5px" />k, n}" src="https://mathworld.wolfram.com/images/equations/SimpleContinuedFraction/Inline22.gif" style="height:15px; width:5px" />], where 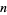 may be Infinity.

REFERENCES:

Rockett, A. M. and Szüsz, P. Continued Fractions. New York: World Scientific, 1992.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشؤون الدينية يوزع أكثر من ألفي وجبة طعام للمعزين في ذكرى عاشوراء بنينوى

قسم الشؤون الطبية يواصل تقديم خدماته الصحية لزائري عاشوراء

جموع المعزين تحيي مراسم يوم العاشر من شهر المحرم عند المرقدين الطاهرين

قسم العلاقات يطلق محطات فتية الكفيل الثقافية في محافظة نينوى

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد