Ford Circle

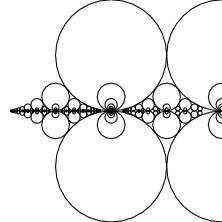
Pick any two relatively prime integers 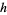 and 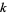, then the circle  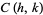of radius  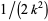centered at  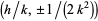is known as a Ford circle. No matter what and how many 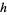s and 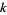s are picked, none of the Ford circles intersect (and all are tangent to the x-axis). This can be seen by examining the squared distance between the centers of the circles with  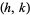and ,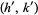

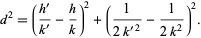(1)

Let 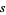 be the sum of the radii

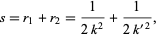(2)

then

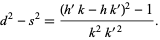(3)

But 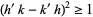, so 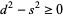 and the distance between circle centers is  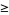the sum of the circle radii, with equality (and therefore tangency) iff 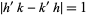. Ford circles are related to the Farey sequence (Conway and Guy 1996).

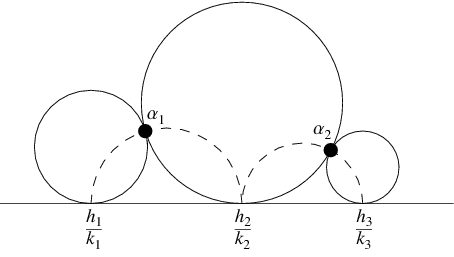
If 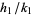, , 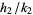and 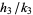 are three consecutive terms in a Farey sequence, then the circles  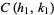and 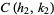 are tangent at

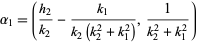(4)

and the circles 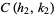 and 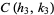 intersect in

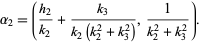(5)

Moreover, 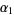 lies on the circumference of the semicircle with diameter  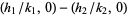and 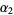 lies on the circumference of the semicircle with diameter  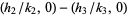(Apostol 1997, p. 101).

REFERENCES:

Apostol, T. M. "Ford Circles." §5.5 in Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 99-102, 1997.

Conway, J. H. and Guy, R. K. "Farey Fractions and Ford Circles." The Book of Numbers. New York: Springer-Verlag, pp. 152-154, 1996.

Ford, L. R. "Fractions." Amer. Math. Monthly 45, 586-601, 1938.

Pickover, C. A. "Fractal Milkshakes and Infinite Archery." Ch. 14 in Keys to Infinity. New York: W. H. Freeman, pp. 117-125, 1995.

Rademacher, H. Higher Mathematics from an Elementary Point of View. Boston, MA: Birkhäuser, 1983.