Anomalous Cancellation

Anomalous cancellation is a "canceling" of digits of 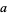 and 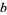 in the numerator and denominator of a fraction  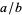which results in a fraction equal to the original. Note that if there are multiple but differing counts of one or more digits in the numerator and denominator there is ambiguity about which digits to cancel, so it is simplest to exclude such cases from consideration.

There are exactly four anomalous cancelling proper fractions having two-digit base-10 numerator and denominator:

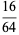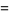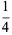			(1)
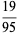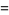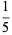			(2)
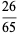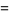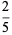			(3)
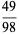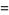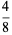			(4)

(c.f. Boas 1979). The first few 3-digit anomalous cancelling numbers are

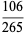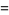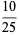			(5)
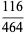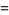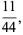			(6)

and the first few with four digits are

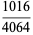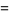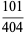			(7)
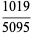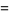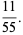			(8)

The numbers of anomalously cancelling proper fractions having 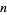 digits in both numerator and denominator for 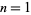, 2, ... are 0, 4, 161, 1851, ....

The numbers of anomalously cancelling proper fractions having 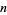 or fewer digits in both numerator and denominator for 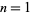, 2, ... are 0, 4, 190, 2844, ....

The concept of anomalous cancellation can be extended to arbitrary bases. For two-digit anomalous cancellation, anomalously cancelling fractions correspond to solutions to

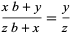(9)

for integers 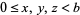. Prime bases  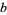have no two-digit solutions, but there is a solution corresponding to each proper divisor of a composite 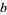. When  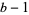is prime, this type of solution is the only one. For base 4, for example, the only two-digit solution is 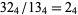. The number of solutions is even unless  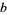is an even square. Boas (1979) gives a table of solutions for 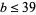. For the first few composite bases 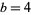, 6, 8, 9, ..., the numbers of two-digit solutions are 1, 2, 2, 2, 4, 4, 2, 6, 7, 4, 4, 10, 6, 6, 6, 4, 6, 10, 6, 4, 8, 6, 6, 21, 2, 6, ... (OEIS A259981).

REFERENCES:

Boas, R. P. "Anomalous Cancellation." Ch. 6 in Mathematical Plums (Ed. R. Honsberger). Washington, DC: Math. Assoc. Amer., pp. 113-129, 1979.

Moessner, A. Scripta Math. 19.

Moessner, A. Scripta Math. 20.

Ogilvy, C. S. and Anderson, J. T. Excursions in Number Theory. New York: Dover, pp. 86-87, 1988.

Sloane, N. J. A. Sequence A259981 in "The On-Line Encyclopedia of Integer Sequences."

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, pp. 26-27, 1986.