المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Racah Polynomial |
 1099
 05:47 مساءً
date: 22-9-2019 |
Author : Koekoek, R. and Swarttouw, R. F. 
Book or Source : "Racah." §1.2 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its q-Analogue. Delft, Netherlands: Technische Universiteit Delft,... 
Page and Part : Report 98-17, pp. 26-29|
Read More
Date: 22-6-2019
2078
Date: 25-4-2019
2183
Date: 11-6-2019
1065
|
A hypergeometric class of orthogonal polynomials defined by
 |
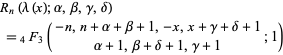(1) |
for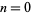 
, 1, ..., 
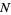, where 
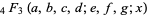is a generalized hypergeometric function,
 |
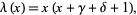(2) |
and one of the following holds
 |
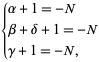(3) |
with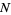 
a nonnegative integer.
REFERENCES:
Koekoek, R. and Swarttouw, R. F. "Racah." §1.2 in The Askey-Scheme of Hypergeometric Orthogonal Polynomials and its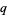 
-Analogue. Delft, Netherlands: Technische Universiteit Delft, Faculty of Technical Mathematics and Informatics Report 98-17, pp. 26-29, 1998.
|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|
