المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Watson-Whipple Transformation |
 1308
 04:30 مساءً
date: 2-9-2019 |
Author : Gasper, G. and Rahman, M. 
Book or Source : Basic Hypergeometric Series. Cambridge, England: Cambridge University Press 
Page and Part : ...|
Read More
Date: 13-6-2019
2943
Date: 30-3-2019
1646
Date: 30-3-2019
1457
|
If at least one of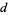 
, 
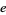, or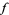 
has the form 
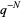for some nonnegative integer 
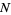(in which case both sums terminate after 
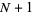terms), then
![_8phi_7[a,qa^(1/2),-qa^(1/2),b,c,d,e,f; a^(1/2),-a^(1/2),(aq)/b,(aq)/c,(aq)/d,(aq)/e,(aq)/f;q,(a^2q^2)/(bcdef)]
=((aq,(aq)/(de),(aq)/(df),(aq)/(ef))_infty)/(((aq)/d,(aq)/e,(aq)/f,(aq)/(def))_infty)_4phi_3[(aq)/(bc),d,e,f; (aq)/b,(aq)/c,(def)/a;q,q],](http://mathworld.wolfram.com/images/equations/Watson-WhippleTransformation/NumberedEquation1.gif) |
where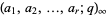 
is a generalized q-Pochhammer symbol
 |
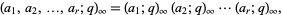and each of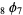 
and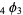 
is a q-hypergeometric function.
REFERENCES:
Gasper, G. and Rahman, M. Basic Hypergeometric Series. Cambridge, England: Cambridge University Press, p. 242, 1990.
Gordon, B. and McIntosh, R. J. "Some Eighth Order Mock Theta Functions." J. London Math. Soc. 62, 321-335, 2000.
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|
