


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-9-2019
Date: 22-7-2019
Date: 30-6-2019
|
Let 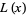 denote the Rogers L-function defined in terms of the usual dilogarithm by
denote the Rogers L-function defined in terms of the usual dilogarithm by
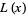 |
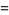 |
![6/(pi^2)[Li_2(x)+1/2lnxln(1-x)]](http://mathworld.wolfram.com/images/equations/AbelsFunctionalEquation/Inline4.gif) |
(1) |
 |
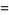 |
![6/(pi^2)[sum_(n=1)^(infty)(x^n)/(n^2)+1/2lnxln(1-x)],](http://mathworld.wolfram.com/images/equations/AbelsFunctionalEquation/Inline7.gif) |
(2) |
then 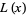 satisfies the functional equation
satisfies the functional equation
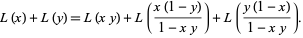 |
(3) |
Abel's duplication formula follows from this identity.
REFERENCES:
Abel, N. H. Oeuvres Completes, Vol. 2 (Ed. L. Sylow and S. Lie). New York: Johnson Reprint Corp., pp. 189-192, 1988.
Bytsko, A. G. "Two-Term Dilogarithm Identities Related to Conformal Field Theory." 9 Nov 1999. http://arxiv.org/abs/math-ph/9911012.
Gordon, B. and McIntosh, R. J. "Algebraic Dilogarithm Identities." Ramanujan J. 1, 431-448, 1997.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 14 and 21, 1999.
Rogers, L. J. "On Function Sum Theorems Connected with the Series 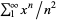 ." Proc. London Math. Soc. 4, 169-189, 1907.
." Proc. London Math. Soc. 4, 169-189, 1907.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|