


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-6-2019
Date: 5-9-2019
Date: 23-8-2018
|
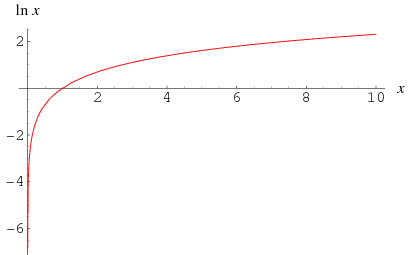
The natural logarithm 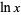 is the logarithm having base e, where
is the logarithm having base e, where
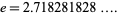 |
(1) |
This function can be defined
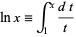 |
(2) |
for 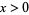 .
.
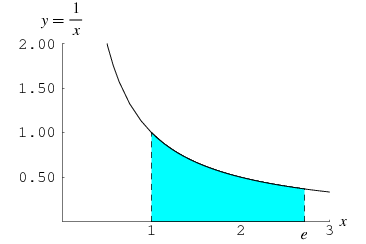
This definition means that e is the unique number with the property that the area of the region bounded by the hyperbola 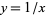 , the x-axis, and the vertical lines
, the x-axis, and the vertical lines 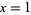 and
and 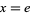 is 1. In other words,
is 1. In other words,
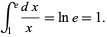 |
(3) |
The notation 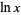 is used in physics and engineering to denote the natural logarithm, while mathematicians commonly use the notation
is used in physics and engineering to denote the natural logarithm, while mathematicians commonly use the notation 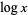 . In this work,
. In this work, 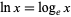 denotes a natural logarithm, whereas
denotes a natural logarithm, whereas 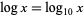 denotes the common logarithm.
denotes the common logarithm.
There are a number of notational conventions in common use for indication of a power of a natural logarithm. While some authors use 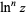 (i.e., using a trigonometric function-like convention), it is also common to write
(i.e., using a trigonometric function-like convention), it is also common to write 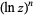 .
.
Common and natural logarithms can be expressed in terms of each other as
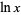 |
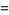 |
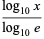 |
(4) |
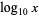 |
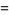 |
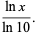 |
(5) |
The natural logarithm is especially useful in calculus because its derivative is given by the simple equation
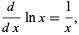 |
(6) |
whereas logarithms in other bases have the more complicated derivative
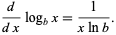 |
(7) |
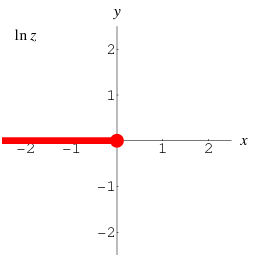
The natural logarithm can be analytically continued to complex numbers as
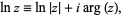 |
(8) |
where 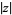 is the complex modulus and
is the complex modulus and 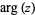 is the complex argument. The natural logarithm is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at
is the complex argument. The natural logarithm is a multivalued function and hence requires a branch cut in the complex plane, which the Wolfram Language's convention places at ![(-infty,0]](http://mathworld.wolfram.com/images/equations/NaturalLogarithm/Inline20.gif) .
.
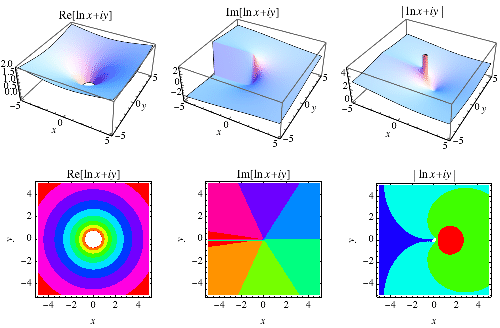 |
The principal value of the natural logarithm is implemented in the Wolfram Language as Log[x], which is equivalent to Log[E, x]. This function is illustrated above in the complex plane.
Note that the inverse trigonometric and inverse hyperbolic functions can be expressed (and, in fact, are commonly defined) in terms of the natural logarithm, as summarized in the table below. Therefore, once these definition are agreed upon, the branch cutstructure adopted for the natural logarithm fixes the branch cuts of these functions.
| function | symbol | definition |
| inverse cosecant | 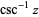 |
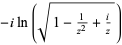 |
| inverse cosine | 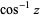 |
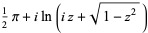 |
| inverse cotangent | 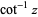 |
![1/2i[ln((z-i)/z)-ln((z+i)/z)]](http://mathworld.wolfram.com/images/equations/NaturalLogarithm/Inline26.gif) |
| inverse hyperbolic cosecant | 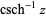 |
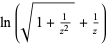 |
| inverse hyperbolic cosine | 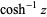 |
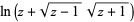 |
| inverse hyperbolic cotangent | 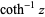 |
![1/2[ln(1+1/z)-ln(1-1/z)]](http://mathworld.wolfram.com/images/equations/NaturalLogarithm/Inline32.gif) |
| inverse hyperbolic secant | 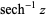 |
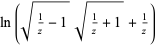 |
| inverse hyperbolic sine | 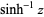 |
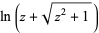 |
| inverse hyperbolic tangent | 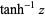 |
![1/2[ln(1+z)-ln(1-z)]](http://mathworld.wolfram.com/images/equations/NaturalLogarithm/Inline38.gif) |
| inverse secant | 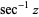 |
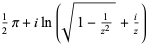 |
| inverse sine | 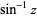 |
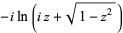 |
| inverse tangent | 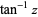 |
![1/2i[ln(1-iz)-ln(1+iz)]](http://mathworld.wolfram.com/images/equations/NaturalLogarithm/Inline44.gif) |
The Mercator series
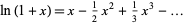 |
(9) |
gives a Taylor series for the natural logarithm.
Continued fraction representations of logarithmic functions include
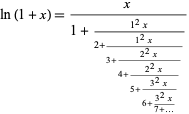 |
(10) |
(Lambert 1770; Lagrange 1776; Olds 1963, p. 138; Wall 1948, p. 342) and
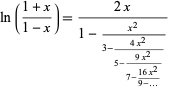 |
(11) |
(Euler 1813-1814; Wall 1948, p. 343; Olds 1963, p. 139).
For a complex number 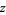 , the natural logarithm satisfies
, the natural logarithm satisfies
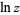 |
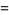 |
![ln[re^(i(theta+2npi))]](http://mathworld.wolfram.com/images/equations/NaturalLogarithm/Inline48.gif) |
(12) |
 |
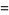 |
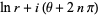 |
(13) |
and
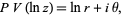 |
(14) |
where 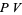 is the principal value.
is the principal value.
Some special values of the natural logarithm include
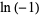 |
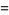 |
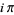 |
(15) |
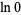 |
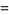 |
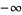 |
(16) |
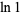 |
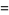 |
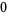 |
(17) |
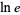 |
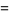 |
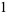 |
(18) |
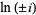 |
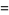 |
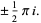 |
(19) |
Natural logarithms can sometimes be written as a sum or difference of "simpler" logarithms, for example
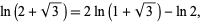 |
(20) |
which follows immediately from the identity
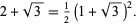 |
(21) |
Plouffe (2006) found the following beautiful identities:
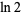 |
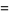 |
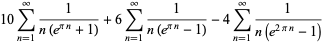 |
(22) |
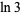 |
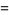 |
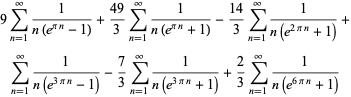 |
(23) |
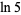 |
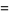 |
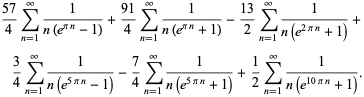 |
(24) |
REFERENCES:
Euler, L. "Commentatio in fractionem continuam qua illustris La Grange potestates binomiales expressit." Mém. de l'Acad. imperiale des sciences de St. Pétersbourg 6, 1813-1814.
Lagrange, J.-L. "Sur l'usage des fractions continues dans le calcul intégral." Nouv. mém. de l'académie royale des sciences et belles-lettres Berlin, 236-264, 1776. Reprinted in Oeuvres, Vol. 4, pp. 301-302.
Lambert, J. L. Beiträge zum Gebrauch der Mathematik und deren Anwendung. Theil 2. Berlin, 1770.
Olds, C. D. Continued Fractions. New York: Random House, 1963.
Plouffe, S. "Identities Inspired from Ramanujan Notebooks (Part 2)." Apr. 2006. http://www.lacim.uqam.ca/~plouffe/inspired2.pdf.
Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae, 30th ed. Boca Raton, FL: CRC Press, 1996.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
قسم الشؤون الفكرية والثقافية يجري اختبارات مسابقة حفظ دعاء أهل الثغور
|
|
|