


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-10-2019
Date: 16-8-2018
Date: 18-6-2019
|
A special case of the confluent hypergeometric function of the first kind. It gives the solution to the radial Schrödinger equation in the Coulomb potential (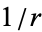 ) of a point nucleus
) of a point nucleus
![(d^2W)/(drho^2)+[1-(2eta)/rho-(L(L+1))/(rho^2)]W=0](http://mathworld.wolfram.com/images/equations/CoulombWaveFunction/NumberedEquation1.gif) |
(1) |
(Abramowitz and Stegun 1972; Zwillinger 1997, p. 122). The complete solution is
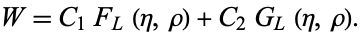 |
(2) |
The Coulomb function of the first kind is
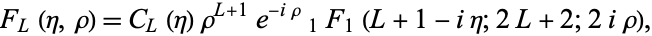 |
(3) |
where
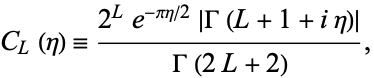 |
(4) |
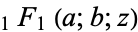 is the confluent hypergeometric function of the first kind,
is the confluent hypergeometric function of the first kind, 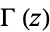 is the gamma function, and the Coulomb function of the second kind is
is the gamma function, and the Coulomb function of the second kind is
![G_L(eta,rho)=(2eta)/(C_0^2(eta))F_L(eta,rho)[ln(2rho)+(q_L(eta))/(p_L(eta))]
+1/((2L+1)C_L(eta))rho^(-L)sum_(K=-L)^inftya_k^L(eta)rho^(K+L),](http://mathworld.wolfram.com/images/equations/CoulombWaveFunction/NumberedEquation5.gif) |
(5) |
where 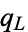 ,
, 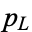 , and
, and 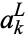 are defined in Abramowitz and Stegun (1972, p. 538).
are defined in Abramowitz and Stegun (1972, p. 538).
REFERENCES:
Abramowitz, M. and Antosiewicz, H. A. "Coulomb Wave Functions in the Transition Region." Phys. Rev. 96, 75-77, 1954.
Abramowitz, M. and Rabinowitz, P. "Evaluation of Coulomb Wave Functions along the Transition Line." Phys. Rev. 96, 77-79, 1954.
Abramowitz, M. and Stegun, I. A. (Eds.). "Coulomb Wave Functions." Ch. 14 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 537-544, 1972.
Biedenharn, L. C.; Gluckstern, R. L.; Hull, M. H. Jr.; and Breit, G. "Coulomb Wave Functions for Large Charges and Small Velocities." Phys. Rev. 97, 542-554, 1955.
Bloch, I.; Hull, M. H. Jr.; Broyles, A. A.; Bouricius, W. G.; Freeman, B. E.; and Breit, G. "Coulomb Functions for Reactions of Protons and Alpha-Particles with the Lighter Nuclei." Rev. Mod. Phys. 23, 147-182, 1951.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 631-633, 1953.
National Bureau of Standards. Tables of Coulomb Wave Functions, Vol. 1, Applied Math Series 17. Washington, DC: U.S. Government Printing Office, 1952.
Stegun, I. A. and Abramowitz, M. "Generation of Coulomb Wave Functions by Means of Recurrence Relations." Phys. Rev. 98, 1851-1852, 1955.
Zwillinger, D. Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, 1997.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
وفد العتبة الكاظمية المقدسة يزور عائلة الشهيد البطل النقيب حارث السوداني
|
|
|