


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-8-2019
Date: 19-9-2019
Date: 13-8-2018
|
A theorem of fundamental importance in spectroscopy and angular momentum theory which provides both (1) an explicit form for the dependence of all matrix elements of irreducible tensors on the projection quantum numbers and (2) a formal expression of the conservation laws of angular momentum (Rose 1995).
The theorem states that the dependence of the matrix element 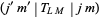 on the projection quantum numbers is entirely contained in the Wigner 3j-symbol (or, equivalently, the Clebsch-Gordan coefficient), given by
on the projection quantum numbers is entirely contained in the Wigner 3j-symbol (or, equivalently, the Clebsch-Gordan coefficient), given by
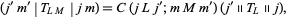 |
where 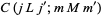 is a Clebsch-Gordan coefficient and
is a Clebsch-Gordan coefficient and 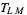 is a set of tensor operators (Rose 1995, p. 85).
is a set of tensor operators (Rose 1995, p. 85).
REFERENCES:
Cohen-Tannoudji, C.; Diu, B.; and Laloë, F. "Vector Operators: The WIgner-Eckart Theorem." Complement 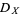 in Quantum Mechanics, Vol. 2. New York: Wiley, pp. 1048-1058, 1977.
in Quantum Mechanics, Vol. 2. New York: Wiley, pp. 1048-1058, 1977.
Eckart, C. "The Application of Group Theory to the Quantum Dynamics of Monatomic Systems." Rev. Mod. Phys. 2, 305-380, 1930.
Edmonds, A. R. Angular Momentum in Quantum Mechanics, 2nd ed., rev. printing. Princeton, NJ: Princeton University Press, 1968.
Gordy, W. and Cook, R. L. Microwave Molecular Spectra, 3rd ed. New York: Wiley, p. 807, 1984.
Messiah, A. "Representation of Irreducible Tensor Operators: Wigner-Eckart Theorem." §32 in Quantum Mechanics, Vol. 2.Amsterdam, Netherlands: North-Holland, pp. 573-575, 1962.
Rose, M. E. "The Wigner-Eckart Theorem." §19 in Elementary Theory of Angular Momentum. New York: Dover, pp. 85-94, 1995.
Shore, B. W. and Menzel, D. H. "Tensor Operators and the Wigner-Eckart Theorem." §6.4 in Principles of Atomic Spectra. New York: Wiley, pp. 285-294, 1968.
Wigner, E. P. "Einige Folgerungen aus der Schrödingerschen Theorie für die Termstrukturen." Z. Physik 43, 624-652, 1927.
Wigner, E. P. Group Theory and Its Application to the Quantum Mechanics of Atomic Spectra, expanded and improved ed. New York: Academic Press, 1959.
Wybourne, B. G. Symmetry Principles and Atomic Spectroscopy. New York: Wiley, pp. 89 and 93-96, 1970.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|