Spherical Hankel Function of the Second Kind

The spherical Hankel function of the second kind 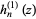 is defined by

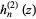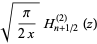			(1)
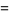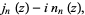			(2)

where 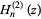 is the Hankel function of the second kind 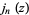and  and 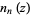 are the spherical Bessel functions of the first and second kinds.

It is implemented in Wolfram Language Version 6 as SphericalHankelH2[n, z].

Explicitly, the first few are given by

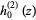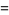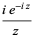			(3)
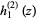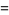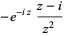			(4)
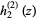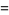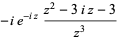			(5)
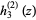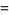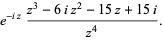			(6)

The derivative is given by

(7)

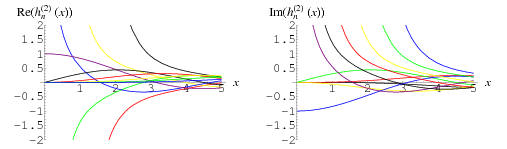
The plot above shows the real and imaginary parts of  on the real axis for , 1, ..., 5.

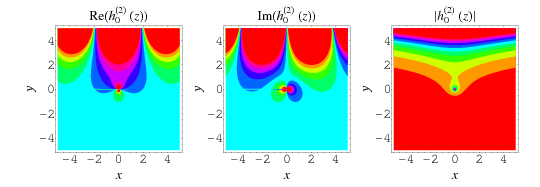
The plots above shows the real and imaginary parts of 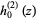 in the complex plane.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Spherical Bessel Functions." §10.1 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 437-442, 1972.

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 623, 1985.