
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-1-2019
Date: 6-3-2017
Date: 17-1-2019
|
 |
The xi-function is the function
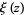 |
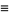 |
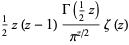 |
(1) |
 |
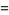 |
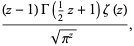 |
(2) |
where 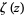 is the Riemann zeta function and
is the Riemann zeta function and 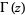 is the gamma function (Gradshteyn and Ryzhik 2000, p. 1076; Hardy 1999, p. 41; Edwards 2001, p. 16). This is a variant of the function originally defined by Riemann in his landmark paper (Riemann 1859), where the above now standard notation follows Landau (Edwards 2001, p. 16).
is the gamma function (Gradshteyn and Ryzhik 2000, p. 1076; Hardy 1999, p. 41; Edwards 2001, p. 16). This is a variant of the function originally defined by Riemann in his landmark paper (Riemann 1859), where the above now standard notation follows Landau (Edwards 2001, p. 16).
It is an entire function (Edwards 2001, p. 16).
It is implemented in the Wolfram Language as RiemannXi[s].
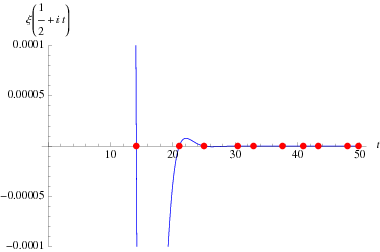
The zeros of 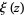 and of its derivatives are all located on the critical strip
and of its derivatives are all located on the critical strip 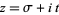 , where
, where 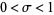 . Therefore, the nontrivial zeros of the Riemann zeta function exactly correspond to those of
. Therefore, the nontrivial zeros of the Riemann zeta function exactly correspond to those of 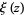 (i.e., the roots of
(i.e., the roots of 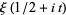 are the same as those of
are the same as those of 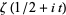 for real
for real 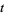 ), with the additional benefit that
), with the additional benefit that 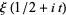 is purely real.
is purely real.
The first few zeros occur at the values summarized in the following table (Wagon 1991, pp. 361-362 and 367-368; Havil 2003, p. 196; Odlyzko), where the corresponding negative values are also roots. The integers closest to these values are 14, 21, 25, 30, 33, 38, 41, 43, 48, 50, ... (OEIS A002410). The numbers of zeros less than 10, 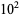 ,
, 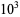 , ... are 0, 29, 649, 10142, 138069, 1747146, ... (OEIS A072080; Odlyzko).
, ... are 0, 29, 649, 10142, 138069, 1747146, ... (OEIS A072080; Odlyzko).
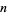 |
Sloane | 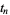 |
| 1 | A058303 | 14.134725 |
| 2 | 21.022040 | |
| 3 | 25.010858 | |
| 4 | 30.424876 | |
| 5 | 32.935062 | |
| 6 | 37.586178 |
Special values include
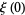 |
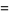 |
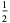 |
(3) |
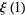 |
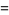 |
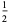 |
(4) |
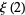 |
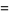 |
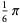 |
(5) |
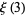 |
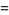 |
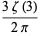 |
(6) |
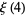 |
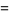 |
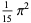 |
(7) |
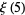 |
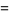 |
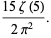 |
(8) |
The 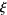 function satisfies the functional equation
function satisfies the functional equation
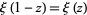 |
(9) |
(Edwards 2001, p. 16).
The xi-function has the Taylor series about 1/2 of
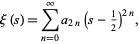 |
(10) |
where
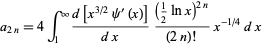 |
(11) |
and
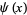 |
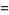 |
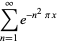 |
(12) |
 |
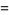 |
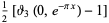 |
(13) |
(Edwards 2001, p. 15), with 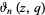 a Jacobi theta function. The coefficient
a Jacobi theta function. The coefficient 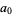 has the simple analytic form
has the simple analytic form
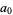 |
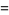 |
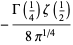 |
(14) |
 |
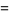 |
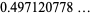 |
(15) |
(OEIS A114720).
As stated by Riemann (1859) and first rigorously proved by Hadamard (1893), the xi-function can be written as
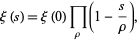 |
(16) |
where the product runs over the roots 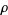 of
of 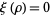 (Edwards 2001, pp. 17-21).
(Edwards 2001, pp. 17-21).
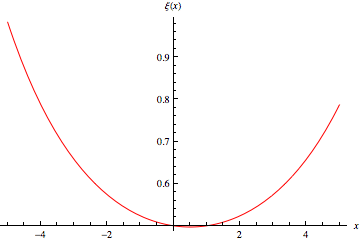
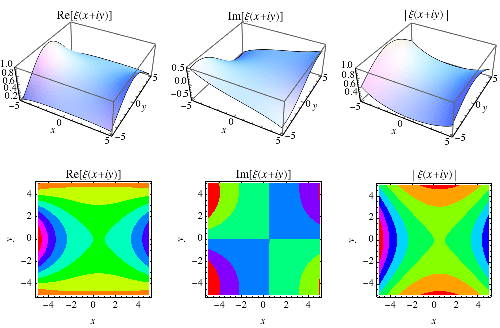 |
The xi-function extended into the complex plane is illustrated above.
The function 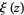 is related to
is related to
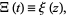 |
(17) |
where 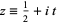 (Gradshteyn and Ryzhik 2000, p. 1074; Edwards 2001, p. 16), which is the function originally considered and actually denoted
(Gradshteyn and Ryzhik 2000, p. 1074; Edwards 2001, p. 16), which is the function originally considered and actually denoted 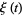 by Riemann (Edwards 2001, p. 16). This function can also be defined as
by Riemann (Edwards 2001, p. 16). This function can also be defined as
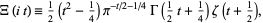 |
(18) |
giving
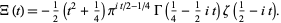 |
(19) |
The de Bruijn-Newman constant is defined in terms of the 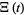 function.
function.
Hardy (1914) proved that 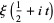 has infinitely many real roots (Hardy's theorem), Hardy and Littlewood (1921) proves that the number of real roots between 0 and
has infinitely many real roots (Hardy's theorem), Hardy and Littlewood (1921) proves that the number of real roots between 0 and 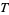 is at least
is at least 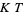 for some positive constant
for some positive constant 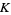 and all sufficiently large
and all sufficiently large 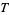 , and Selberg (1942) proved that this number is in fact at least
, and Selberg (1942) proved that this number is in fact at least 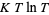 for some positive
for some positive 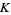 and all large
and all large 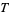 (Edwards 2001, p. 19).
(Edwards 2001, p. 19).
Coffey (2004) gives a number of formulas of derivatives of 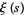 .
.
REFERENCES:
Borwein, J. M.; Bradley, D. M.; and Crandall, R. E. "Computational Strategies for the Riemann Zeta Function." J. Comput. Appl. Math. 121, 247-296, 2000.
Brent, R. P. "On the Zeros of the Riemann Zeta Function in the Critical Strip." Math. Comput. 33, 1361-1372, 1979.
Brent, R. P.; van de Lune, J.; te Riele, H. J. J.; and Winter, D. T. "On the Zeros of the Riemann Zeta Function in the Critical Strip. II." Math. Comput. 39, 681-688, 1982.
Coffey, M. W. "Relations and Positivity Results for Derivatives of the Riemann 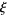 Function." J. Comput. Appl. Math. 166, 525-534, 2004.
Function." J. Comput. Appl. Math. 166, 525-534, 2004.
Conrey, J. B. "The Riemann Hypothesis." Not. Amer. Math. Soc. 50, 341-353, 2003. http://www.ams.org/notices/200303/fea-conrey-web.pdf.
Edwards, H. M. "The Function 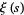 ." §1.8 in Riemann's Zeta Function. New York: Dover, pp. 16-18, 2001.
." §1.8 in Riemann's Zeta Function. New York: Dover, pp. 16-18, 2001.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, corr. enl. 4th ed. San Diego, CA: Academic Press, 2000.
Hadamard, J. "Étude sur les propriétés des fonctions entières et en particulier d'une fonction considérée par Riemann." J. math. pures appl. 9, 171-215, 1893.
Hardy, G. H. "Sur les zéros de la fonction 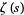 de Riemann." C. R. Acad. Sci. Paris 158, 1012-1014, 1914.
de Riemann." C. R. Acad. Sci. Paris 158, 1012-1014, 1914.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, 1999.
Hardy, G. H. and Littlewood, J. E. "The Zeros of Riemann's Zeta-Function on the Critical Line." Math. Z. 10, 283-317, 1921.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 202-203, 2003.
Keiper, J. B. "Power Series Expansions of Riemann's 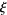 Function." Math. Comput. 58, 765-773, 1992.
Function." Math. Comput. 58, 765-773, 1992.
Li, X.-J. "The Positivity of a Sequence of Numbers and the Riemann Hypothesis." J. Number Th. 65, 325-333, 1997.
Odlyzko, A. M. "The 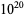 th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors." Preprint.
th Zero of the Riemann Zeta Function and 70 Million of Its Neighbors." Preprint.
Odlyzko, A. "Tables of Zeros of the Riemann Zeta Function." http://www.dtc.umn.edu/~odlyzko/zeta_tables/.
Riemann, G. F. B. "Über die Anzahl der Primzahlen unter einer gegebenen Grösse." Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 671-680, Nov. 1859.
Reprinted in Das Kontinuum und Andere Monographen (Ed. H. Weyl). New York: Chelsea, 1972. Also reprinted in English translation in Edwards, H. M. Appendix. Riemann's Zeta Function. New York: Dover, pp. 299-305, 2001.
Selberg, A. "On the Zeros of Riemann's Zeta-Function." Skr. Norske Vid.-Akad. Oslo, No. 10, 1942.
Sloane, N. J. A. Sequences A002410, A058303, A072080, and A114720 in "The On-Line Encyclopedia of Integer Sequences."
Titchmarsh, E. C. The Theory of the Riemann Zeta Function, 2nd ed. New York: Clarendon Press, 1987.
Wagon, S. "The Evidence: Where Are the Zeros of Zeta of 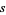 ?" Math. Intel. 8, 57-62, 1986.
?" Math. Intel. 8, 57-62, 1986.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, 1991.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ضمن مشروع الورود الفاطمية بنسخته السابعة شعبة الخطابة النسوية تقدّم محاضرات إرشادية لعدد من المدارس المشاركة في حفل التكليف الشرعي
|
|
|