المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Newton-Girard Formulas |
 1263
 02:53 مساءً
date: 13-2-2019 |
Author : Séroul, R 
Book or Source : "Newton-Girard Formulas." §10.12 in Programming for Mathematicians. Berlin: Springer-Verlag 
Page and Part : pp. 278-279|
Read More
Date: 13-2-2019
749
Date: 6-3-2017
1382
Date: 17-1-2019
1206
|
The identities between the symmetric polynomials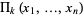 
and the sums of 
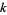th powers of their variables
 |
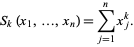(1) |
The identities are given by
 |
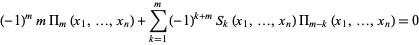(2) |
for each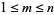 
and for an arbitrary number of variables 
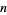. The first few identities are
 |
 |
 |
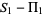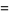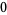(3) |
 |
 |
 |
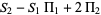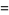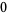(4) |
 |
 |
 |
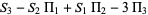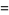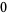(5) |
 |
 |
 |
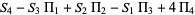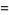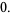(6) |
REFERENCES:
Séroul, R. "Newton-Girard Formulas." §10.12 in Programming for Mathematicians. Berlin: Springer-Verlag, pp. 278-279, 2000.
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|
