


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-3-2017
Date: 6-3-2017
Date: 17-2-2019
|
Let 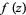 be an entire function such that
be an entire function such that 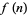 is an integer for each positive integer
is an integer for each positive integer 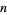 . Then Pólya (1915) showed that if
. Then Pólya (1915) showed that if
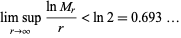 |
(1) |
(OEIS A002162), where
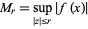 |
(2) |
is the supremum, then 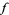 is a polynomial. Furthermore,
is a polynomial. Furthermore, 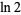 is the best constant (i.e., counterexamples exist for every smaller value).
is the best constant (i.e., counterexamples exist for every smaller value).
If 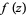 is an entire function with
is an entire function with 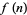 a Gaussian integer for each Gaussian integer
a Gaussian integer for each Gaussian integer 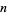 , then Gelfond (1929) proved that there exists a constant
, then Gelfond (1929) proved that there exists a constant 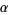 such that
such that
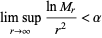 |
(3) |
implies that 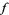 is a polynomial. Gramain (1981, 1982) showed that the best such constant is
is a polynomial. Gramain (1981, 1982) showed that the best such constant is
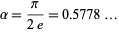 |
(4) |
(OEIS A086056).
Maser (1980) proved the weaker result that 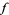 must be a polynomial if
must be a polynomial if
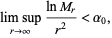 |
(5) |
where
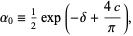 |
(6) |
and
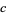 |
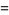 |
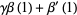 |
(7) |
 |
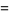 |
![1/4pi{2gamma+2ln2+3lnpi-4ln[Gamma(1/4)]}](http://mathworld.wolfram.com/images/equations/Masser-GramainConstant/Inline17.gif) |
(8) |
 |
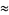 |
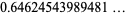 |
(9) |
(OEIS A086057), 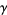 is the Euler-Mascheroni constant,
is the Euler-Mascheroni constant, 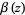 is the Dirichlet beta function,
is the Dirichlet beta function, 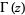 is the gamma function,
is the gamma function,
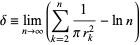 |
(10) |
is known as the Masser-Gramain constant, and 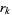 is the minimum nonnegative
is the minimum nonnegative 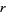 for which there exists a complex number
for which there exists a complex number 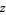 for which the closed disk with center
for which the closed disk with center 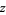 and radius
and radius 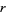 contains at least
contains at least 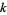 distinct Gaussian integers.
distinct Gaussian integers.
Gramain and Weber (1985, 1987) have obtained
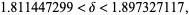 |
(11) |
which implies
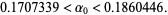 |
(12) |
Gramain (1981, 1982) conjectured that
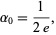 |
(13) |
which would imply
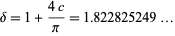 |
(14) |
(OEIS A086058).
REFERENCES:
Finch, S. R. "Masser-Gramain Constant." §7.2 Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 459-461, 2003.
Gosper, R. W. "http://www.mathsoft.com/asolve/constant/constant.html." math-fun@cs.arizona.edu posting, Sept. 27, 1996.
Gel'fond, A. O. "Sur un théorème de M. G. Pólya." Atti Accad. Naz. Lincei Rend. 10, 568-574, 1929.
Gramain, F. "Sur le théorème de Fukagawa-Gel'fond." Invent. Math. 63, 495-506, 1981.
Gramain, F. "Sur le théorème de Fukagawa-Gel'fond-Gruman-Masser." Séminaire Delange-Pisot-Poitou (Théorie des Nombres), 1980-1981. Boston, MA: Birkhäuser, 1982.
Gramain, F. and Weber, M. "Computing and Arithmetic Constant Related to the Ring of Gaussian Integers." Math. Comput. 44, 241-245, 1985.
Gramain, F. and Weber, M. "Computing and Arithmetic Constant Related to the Ring of Gaussian Integers." Math. Comput. 48, 854, 1987.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 116-117, 2003.
Masser, D. W. "Sur les fonctions entières à valeurs entières." C. R. Acad. Sci. Paris Sér. A-B 291, A1-A4, 1980.
Pólya, G. "Über ganzwertige ganze Funktionen." Rend. Circ. Mat. Palermo 40, 1-16, 1915.
Sloane, N. J. A. Sequences A002162/M4074, A086056, A086057, and A086058 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|