
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-10-2018
Date: 24-10-2018
Date: 18-11-2018
|
The three circles theorem, also called Hadamard's three circles theorem (Edwards 2001, p. 187), states that if 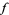 is an analytic function in the annulus
is an analytic function in the annulus 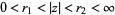 ,
, 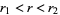 , and
, and 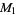 ,
, 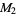 , and
, and 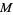 are the maxima of
are the maxima of 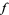 on the three circles corresponding to
on the three circles corresponding to 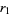 ,
, 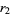 , and
, and 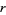 , respectively, then
, respectively, then
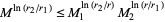 |
(Derbyshire 2004, p. 376).
The theorem was first published by Hadamard in 1896, although without proof (Bohr and Landau 1913; Edwards 2001, p. 187).
REFERENCES:
Bohr, H. and Landau, E. "Beiträge zur Theorie der Riemannschen Zetafunktion." Math. Ann. 74, 3-30, 1913. Reprinted in Bohr, H. §B11 in Collected Works, Vol. 1.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 159 and 376, 2004.
Edwards, H. M. "The Three Circles Theorem." §9.3 in Riemann's Zeta Function. New York: Dover, pp. 187-188, 2001.
Littlewood, J. E. "Quelques conséquences de l'hypothèse que la fonction 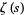 n'a pas de zéros dans le demi-plan
n'a pas de zéros dans le demi-plan 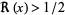 ." C. R. Acad. Sci. Paris 154, 263-266, 1912.
." C. R. Acad. Sci. Paris 154, 263-266, 1912.
Robinson, R. M. "Hadamard's Three Circles Theorem." Bull. Amer. Math. Soc. 50, 795-802, 1944.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|