Frobenius Method

If 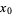 is an ordinary point of the ordinary differential equation, expand  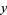in a Taylor series about 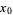. Commonly, the expansion point can be taken as 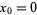, resulting in the Maclaurin series

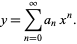(1)

Plug 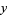 back into the ODE and group the coefficients by power. Now, obtain a recurrence relation for the 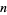th term, and write the series expansion in terms of the 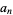s. Expansions for the first few derivatives are

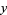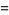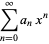			(2)
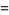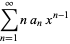			(3)
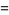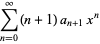			(4)
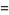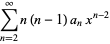			(5)
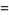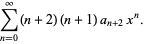			(6)

If 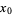 is a regular singular point of the ordinary differential equation,

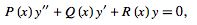(7)

solutions may be found by the Frobenius method or by expansion in a Laurent series. In the Frobenius method, assume a solution of the form

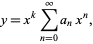(8)

so that

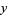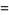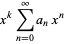			(9)
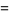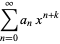			(10)
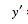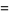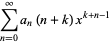			(11)
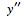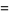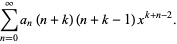			(12)

Now, plug  back into the ODE and group the coefficients by power to obtain a recursion formula for the 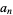th term, and then write the series expansion in terms of the 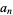s. Equating the  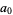term to 0 will produce the so-called indicial equation, which will give the allowed values of  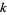in the series expansion.

As an example, consider the Bessel differential equation

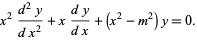(13)

Plugging (◇) into (◇) yields

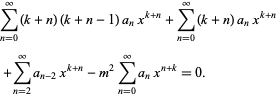(14)

The indicial equation, obtained by setting 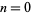, is then

(15)

Since 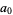 is defined as the first nonzero term, 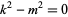, so 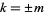. For illustration purposes, ignore  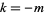and consider only the case  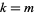(avoiding the special case 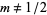), then equation (14) requires that

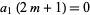(16)

(so 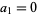) and

(17)

for 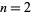, 3, ..., so

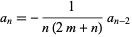(18)

for 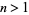. Plugging back in to (◇), rearranging, and simplifying then gives the series solution that defined the Bessel function of the first kind 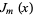, which is the nonsingular solution to (◇). (Considering the case  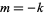proceeds analogously and results in the solution .)

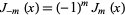Fuchs's theorem guarantees that at least one power series solution will be obtained when applying the Frobenius method if the expansion point is an ordinary, or regular, singular point. For a regular singular point, a Laurent seriesexpansion can also be used. Expand 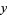 in a Laurent series, letting

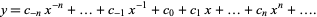(19)

Plug 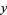 back into the ODE and group the coefficients by power. Now, obtain a recurrence formula for the 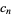th term, and write the Taylor series in terms of the 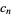s.

REFERENCES:

Arfken, G. "Series Solutions--Frobenius' Method." §8.5 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 454-467, 1985.

Frobenius. "Ueber die Integration der linearen Differentialgleichungen durch Reihen." J. reine angew. Math. 76, 214-235, 1873.

Ince, E. L. Ch. 5 in Ordinary Differential Equations. New York: Dover, 1956.