


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-9-2018
Date: 2-5-2019
Date: 15-9-2019
|
The operator representing the computation of a derivative,
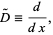 |
(1)
|
sometimes also called the Newton-Leibniz operator. The second derivative is then denoted 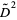 , the third
, the third 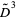 , etc. The integral is denoted
, etc. The integral is denoted 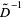 .
.
The differential operator satisfies the identity
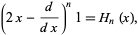 |
(2)
|
where 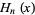 is a Hermite polynomial (Arfken 1985, p. 718), where the first few cases are given explicitly by
is a Hermite polynomial (Arfken 1985, p. 718), where the first few cases are given explicitly by
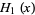 |
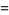 |
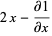 |
(3)
|
 |
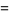 |
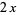 |
(4)
|
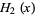 |
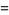 |
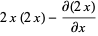 |
(5)
|
 |
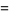 |
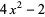 |
(6)
|
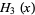 |
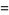 |
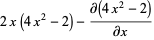 |
(7)
|
 |
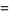 |
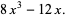 |
(8)
|
The symbol 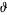 can be used to denote the operator
can be used to denote the operator
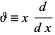 |
(9)
|
(Bailey 1935, p. 8). A fundamental identity for this operator is given by
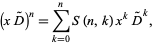 |
(10)
|
where 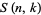 is a Stirling number of the second kind (Roman 1984, p. 144), giving
is a Stirling number of the second kind (Roman 1984, p. 144), giving
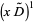 |
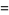 |
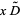 |
(11)
|
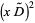 |
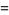 |
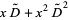 |
(12)
|
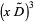 |
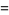 |
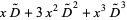 |
(13)
|
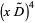 |
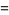 |
 |
(14)
|
and so on (OEIS A008277). Special cases include
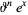 |
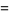 |
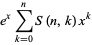 |
(15)
|
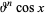 |
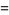 |
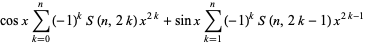 |
(16)
|
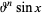 |
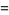 |
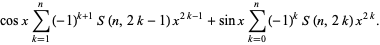 |
(17)
|
A shifted version of the identity is given by
![[(x-a)D^~]^n=sum_(k=0)^nS(n,k)(x-a)^kD^~^k](http://mathworld.wolfram.com/images/equations/DifferentialOperator/NumberedEquation5.gif) |
(18)
|
(Roman 1984, p. 146).
REFERENCES:
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: University Press, 1935.
Roman, S. The Umbral Calculus. New York: Academic Press, pp. 59-63, 1984.
Sloane, N. J. A. Sequence A008277 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|