
Inclusion-Exclusion Principle
 المؤلف:
Andrews, G. E
المؤلف:
Andrews, G. E
 المصدر:
Number Theory. Philadelphia, PA: Saunders
المصدر:
Number Theory. Philadelphia, PA: Saunders
 الجزء والصفحة:
...
الجزء والصفحة:
...
 29-12-2021
29-12-2021
 1789
1789
Inclusion-Exclusion Principle
Let 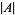 denote the cardinal number of set
denote the cardinal number of set 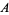 , then it follows immediately that
, then it follows immediately that
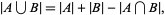 |
(1)
|
where 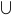 denotes union, and
denotes union, and 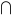 denotes intersection. The more general statement
denotes intersection. The more general statement
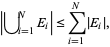 |
(2)
|
also holds, and is known as Boole's inequality or one of the Bonferroni inequalities.
This formula can be generalized in the following beautiful manner. Let ![A=<span style=]() {A_i}_(i=1)^p" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline5.gif" style="height:19px; width:69px" /> be a p-system of
{A_i}_(i=1)^p" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline5.gif" style="height:19px; width:69px" /> be a p-system of 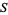 consisting of sets
consisting of sets 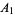 , ...,
, ..., 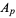 , then
, then
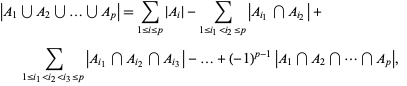 |
(3)
|
where the sums are taken over k-subsets of 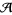 . This formula holds for infinite sets
. This formula holds for infinite sets 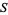 as well as finite sets (Comtet 1974, p. 177).
as well as finite sets (Comtet 1974, p. 177).
The principle of inclusion-exclusion was used by Nicholas Bernoulli to solve the recontres problem of finding the number of derangements (Bhatnagar 1995, p. 8).
For example, for the three subsets ![A_1=<span style=]() {2,3,7,9,10}" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline11.gif" style="height:15px; width:116px" />,
{2,3,7,9,10}" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline11.gif" style="height:15px; width:116px" />, ![A_2=<span style=]() {1,2,3,9}" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline12.gif" style="height:15px; width:94px" />, and
{1,2,3,9}" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline12.gif" style="height:15px; width:94px" />, and ![A_3=<span style=]() {2,4,9,10}" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline13.gif" style="height:15px; width:101px" /> of
{2,4,9,10}" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline13.gif" style="height:15px; width:101px" /> of ![S=<span style=]() {1,2,...,10}" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline14.gif" style="height:15px; width:101px" />, the following table summarizes the terms appearing the sum.
{1,2,...,10}" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline14.gif" style="height:15px; width:101px" />, the following table summarizes the terms appearing the sum.
| # |
term |
set |
length |
| 1 |
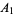 |
![<span style=]() {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline16.gif" style="height:15px; width:5px" />2, 3, 7, 9, 10 {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline16.gif" style="height:15px; width:5px" />2, 3, 7, 9, 10![<span style=]() }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline17.gif" style="height:15px; width:5px" /> }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline17.gif" style="height:15px; width:5px" /> |
5 |
| |
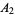 |
![<span style=]() {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline19.gif" style="height:15px; width:5px" />1, 2, 3, 9 {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline19.gif" style="height:15px; width:5px" />1, 2, 3, 9![<span style=]() }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline20.gif" style="height:15px; width:5px" /> }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline20.gif" style="height:15px; width:5px" /> |
4 |
| |
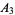 |
![<span style=]() {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline22.gif" style="height:15px; width:5px" />2, 4, 9, 10 {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline22.gif" style="height:15px; width:5px" />2, 4, 9, 10![<span style=]() }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline23.gif" style="height:15px; width:5px" /> }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline23.gif" style="height:15px; width:5px" /> |
4 |
| 2 |
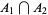 |
![<span style=]() {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline25.gif" style="height:15px; width:5px" />2, 3, 9 {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline25.gif" style="height:15px; width:5px" />2, 3, 9![<span style=]() }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline26.gif" style="height:15px; width:5px" /> }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline26.gif" style="height:15px; width:5px" /> |
3 |
| |
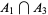 |
![<span style=]() {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline28.gif" style="height:15px; width:5px" />2, 9, 10 {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline28.gif" style="height:15px; width:5px" />2, 9, 10![<span style=]() }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline29.gif" style="height:15px; width:5px" /> }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline29.gif" style="height:15px; width:5px" /> |
3 |
| |
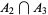 |
![<span style=]() {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline31.gif" style="height:15px; width:5px" />2, 9 {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline31.gif" style="height:15px; width:5px" />2, 9![<span style=]() }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline32.gif" style="height:15px; width:5px" /> }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline32.gif" style="height:15px; width:5px" /> |
2 |
| 3 |
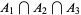 |
![<span style=]() {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline34.gif" style="height:15px; width:5px" />2, 9 {" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline34.gif" style="height:15px; width:5px" />2, 9![<span style=]() }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline35.gif" style="height:15px; width:5px" /> }" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline35.gif" style="height:15px; width:5px" /> |
2 |
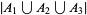 is therefore equal to
is therefore equal to 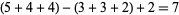 , corresponding to the seven elements
, corresponding to the seven elements ![A_1 union A_2 union A_3=<span style=]() {1,2,3,4,7,9,10}" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline38.gif" style="height:15px; width:212px" />.
{1,2,3,4,7,9,10}" src="https://mathworld.wolfram.com/images/equations/Inclusion-ExclusionPrinciple/Inline38.gif" style="height:15px; width:212px" />.
REFERENCES:
Andrews, G. E. Number Theory. Philadelphia, PA: Saunders, pp. 139-140, 1971.
Andrews, G. E. q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., p. 60, 1986.
Bhatnagar, G. Inverse Relations, Generalized Bibasic Series, and Their U(n) Extensions. Ph.D. thesis. Ohio State University, 1995.
Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, pp. 176-177, 1974.
da Silva. "Proprietades geraes." J. de l'Ecole Polytechnique, cah. 30.
de Quesada, C. A. "Daniel Augusto da Silva e la theoria delle congruenze binomie." Ann. Sci. Acad. Polytech. Porto, Coīmbra 4, 166-192, 1909.
Dohmen, K. Improved Bonferroni Inequalities with Applications: Inequalities and Identities of Inclusion-Exclusion Type. Berlin: Springer-Verlag, 2003.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 66, 2003.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, pp. 178-179, 1997.
Sylvester, J. "Note sur la théorème de Legendre." Comptes Rendus Acad. Sci. Paris 96, 463-465, 1883.
 الاكثر قراءة في نظرية المجموعات
الاكثر قراءة في نظرية المجموعات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


