Ordinal Exponentiation
المؤلف:
Rubin, J. E
المصدر:
Set Theory for the Mathematician. New York: Holden-Day, 1967.
الجزء والصفحة:
...
29-12-2021
1320
Ordinal Exponentiation
Let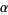 
and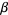 
be any ordinal numbers, then ordinal exponentiation is defined so that if 
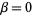then 
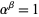. If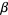 
is not a limit ordinal, then choose 
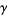such that 
,
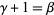If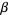 
is a limit ordinal, then 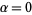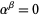if 
, 
. If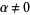 
then,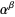 
is the least ordinal greater than any ordinal in the set ![<span style=]()
{alpha^gamma:gamma<beta}" src="https://mathworld.wolfram.com/images/equations/OrdinalExponentiation/Inline13.gif" style="height:15px; width:64px" /> (Rubin 1967, p. 204; Suppes 1972, p. 215).
Note that this definition is not analogous to the definition for cardinals, since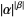 
may not equal 
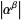, even though 
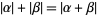and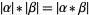 
. Note also that 
.
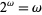A familiar example of ordinal exponentiation is the definition of Cantor's first epsilon number.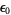 
is the least ordinal such that 
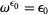. It can be shown that it is the least ordinal greater than any ordinal in ![<span style=]()
{omega,omega^omega,omega^(omega^omega),...}" src="https://mathworld.wolfram.com/images/equations/OrdinalExponentiation/Inline21.gif" style="height:22px; width:101px" />.
REFERENCES:
Rubin, J. E. Set Theory for the Mathematician. New York: Holden-Day, 1967.
Suppes, P. Axiomatic Set Theory. New York: Dover, 1972.
الاكثر قراءة في نظرية المجموعات
اخر الاخبار
اخبار العتبة العباسية المقدسة
