قانون التساقط

عندما تترك حجراً حراً طليقاً تجده يتحرك إلى أسفل بسرعة متزايدة، ولقد حاول غاليليو ان يستنبط القانون الرياضي الذي يتحكم في تلك الحركة ذات السرعة المتزايدة، إلا ان التساقط الحر للأجسام يبلغ من السرعة ما يحول دون دراسته بالتفصيل من غير استعمال الاجهزة الحديثة التي على غرار التصوير مثلاً. ولذلك قرر غاليليو ان يمدد قوى الجاذبية⁽¹⁾ بأن يجعل الكرة تتدحرج من اعلى مستوى مائل ــ شكل (1-1) ، فكلما ازداد ميل المستوى تدحرجت الكرة بسرعة  أكبر. وفي النهاية، عندما يصبح المستوى رأسياً تماماً تسقط الكرة حرة طليقة بمحاذاة المستوى. وكان قياس الزمن الذي تستغرقه الكرة في قطع المسافات المختلفة هو العقبة الأساسية في إجراء هذه التجربة، ولكن غاليليو تغلب على هذه العقبة باستخدام ساعة مائية كان يقدر فيها الزمن بقياس الماس المتدفق من فتحة ضيقة أسفل مستودع كبير. وقد ابتدأ من حالة السكون وعمد إلى عمل علامات توضح الأوضاع المتباينة لكرة خلال فترات متساوية من الزمن، وعند ذلك وجد ان المسافات التي تقطعها الكرة خلال تلك الازمنة المتساوية تحمل فيما بينها النسب 1:3:5:7 ........... الخ ، وعندما زاد ميل المستوى وجد أن المسافات المقطوعة زادت كذلك مع احتفاظها فيما بينها دائماً  بنفس النسب. وفي ضوء هذه النتيجة قرر غاليليو ضرورة صحة هذا القانون في الحالة النهائية التي يصبح فيها المستوى رأسياً فتتساقط الكرة حرة طليقة. ومهما يكن من شيء فإنه يمكن التعبير عن هذه النتيجة بطريقة أخرى رياضية ، وذلك بأن نقول: تتناسب المسافة الكلية التي تقطعها الكرة خلال فترة معينة من الزمن مع مربع الزمن. أو كما كان يعبر عنها في عصر غاليليو : "هو تناسب مزدوج" مع الزمن. وفي الحقيقة لو أننا اتخذنا المسافة كالتي تقطعها الكرة خلال الفترة الأولى من الزمن كوحدة للطول لوجدنا أن المسافة الكلية التي تقطعها الكرة في نهاية الفترات المتتابعة هي بحسب قانون التربيع. 

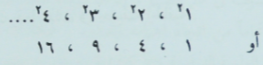
وعلى ذلك تكون المسافة المقطوعة خلال الفترات الزمنية المتتابعة هي:

الشكل (1-1): غاليليو وهو يدرس الحركة ذاتا لسرعة المتزايدة لكرة تتدحرج إلى أسفل مستوى مائل

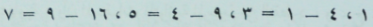⁽²⁾ وهلم جراً.

ومن رصد الكيفية التي ترتبط بها المسافة المقطوعة مع الزمن استنتج غاليليو أنه نسوق هنا برهان هذا الاستنتاج كما صاغه غاليليو نفسه ⁽³⁾:

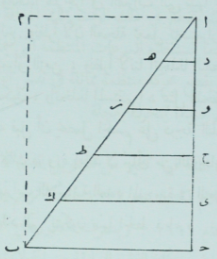
الشكل (1-2): برهان غاليليو على انه في حالة الحركة ذات المجلة (المنتظمة)، عندما تبتدئ من الكسون، تعادل المسافة التي يقطعها الجسم نصف المسافة التي يقطعها أو أنه عبر المسافة كلها بنفس السرعة.

في الحركة بعجلة، عندما تتزايد السرعة بصورة مستمرة،  لا تستطيع تقسيم درجات السرعة (أو قيم السرعة يحسب تعييرنا الحديث) التي تتزايد على الدوام لتصل إلى أي عدد محدود، لأن تغيرها في كل لحظة يجعلها غير محدودة دائماً إلى الأبد. وعلى ذلك يكون من الأسبل لنا ان نضرب لأنفسنا مثلاً على مثلم مثل ا ب جـ ـ شكل (2-5) نأخذ على الضلع ا جـ أي عدد يروق لنا من الأجزاء المتساوية ، مثل ا د ، د و ، و ح ، ح ى ،  ى جـ ، ونرسم من النقط د، و، ح، ى مستقيمات توازي القاعدة ب جـ ثم نتصور ان الأجزاء التي أخذناها على أ جـ هي أزمنة متساوية ، وأن المستقيمات المتوازية المرسومة من النقط د، و، ح، ى تمثل لنا درجات السرعة المتزايدة بعجلة تجعلها تبر بمقادير متساوية في أزمنة متساوية. لتكن النقطة ا هي التي تمثل حالة السكون، فعندما يغادرها الجسم تكون درجة سرعته بعد الزمن أ د هي د هـ . ولنفترض ان السرعة في  الفترة الثانية ازدادت من د هـ إلى و ز ، وهكذا هلم جرا في الفترات التي تليها بحسب زيادة المستقيمات ولا ينقطع عملها باستمرار الزمن، ونظراً لأننا اتخذنا النقطة ا لتمثل أدنى قدر من السرعة، أو حالة السكون، واتخذنا المستقيم ا د  ليمثل اللحظة الأولى من الزمن الذي يليها، فمن الواضح أنه قبل أن يحصل الجسم على درجة السرعة د هـ خلال الفترة ا د ، يتحتم ان يسبق ذلك مروره بعدد لا نهائي من الدرجات الأصغر فالأصغر، التي اكتسبها خلال الفترات اللانهائية العدد الموجودة في الزمن د ا ، تلك التي تقابل النقط غير المحدودة العدد التي يتكون منها الخط د ا .

وعلى ذلك لكي تمثل العدد اللانهائي من درجات السرعة التي تتمخض عنها الدرجة د هـ ، نحتاج إلى تصور مستقيمات تتناقص أطوالها على التدريج ترسل من فقد د ا اللانهائية العدد بحيث توازي د هـ . ويمثل لنا هذا العدد اللانهائي من الخطوط سطح المثلث  ا هـ د. ومعنى هذا أننا قد نتصور أنه خلال أية مسافة يمر بها الجسم، عندما تبدأ الحركة من حالة السكون تحت عجلة منتظمة، يكون قد مر بعدد لا نهائي من درجات السرعة المتزايدة، التي يمثلها عدد لا نهائي من المستقيمات تبدأ من النقطة ا وترسم موازية للمستقيم هـ د ، وباستمرار الحركة يمكن ان تمثل السرعة بالمستقيمات ز و ن ط ح ، ك ى ، . . . وهكذا كما نشاء.

والآن لنكمل متوازى الأضلاع ا م ب جـ ، ثم نمد إلى الضلع ب م كل المستقيمات المتوازية المرسومة في المثلث إلى جانب ذلك العدد اللانهائي من نفس المستقيمات المتوازية المرسومة من جميع النقط التي يتكون منها الضلع ا جـ. فكما يمثل المستقيم ب جـ ، الذي هو أكبر هذه المتوازيات في المثلث، أعظم درجة لسرعة اكتسبها  الجسم المتحرك بعجلة متزايدة، ويمثل جميع سطح المثلث كتلة ومجموع السرعة كلها، التي بها يمر الجسم بهذا الحيز بالذات خلال الزمن ا جـ ، فإن متوازي الأضلاع هو الآن مجموعة وكتلة عدد مماثل من درجات السرعة التي تساوي كل منها أكبر قدر ب جـ . وتعادل هذه الكتلة من درجات السرعة ضعف كتلة السرعة المتزايدة في المثلث، وحتى يعادل متوازى الأضلاع المذكور ضعف المثلث ، مما يدل على ان الجسم المتساقط، عندما يجمع فلا درجات السرعة المتزايدة الممثلة  بالمثلث ا ب جـ ،  بحيث يقطع في ذلك الوقت تلك المسافة، يصبح من المعقول جداً، ومن المحتمل عندما نستخدم السرعات المنتظمة مماثلة في نفس الوقت مسافة تبلغ ضعف تلك التي يقطعها الجسم عندما يتحرك بعجلة.

ورغم ان مثل هذه اللغة فيها كثير من التطويل الذي لا مبرر له، فإننا يجب ان نتذكر ان هذا الكلام كتب عام 1632 ! وبصرف النظر عن أي هذه العبارة هي أول صياغة لقانون التساقط الحر، فإن الفقرة السابقة من المقولات Discorso إنما تتضمن أيضاً أولى خطوات نشوء ما نطلق عليه اسم "حساب التفاضل"، الذي يحصل فيه على النتائج عن طريق تجميع عدد لا نهائي في الكبر لكميات متناهية في الصغر.

وتبعاً لطريقتنا الرياضية الحديثة نستطيع كتابة قانون غاليليو للحركة بعجلة منتظمة على النحو الآتي:

السرعة  = العجلة × الزمن

والمسافة = 1/2 العجلة  × مربع الزمن

وفي حالة التساقط الحر يرمز عادة للعجلة بالحرف جـ (للدلالة على الجاذبية) وهي تساوي 981 سنتيمتراً في الثانية في الثانية . وهي تعنى انه في كل ثانية، بعد ان يشرع الجسم في السقوط، تتزايد سرعته بمقدار 981 سنتيمتراً في الثانية. وباستخدام الوحدات الإنجليزية ــ الأمريكية تعادل العجلة جـ 32,2 قدماً في الثانية في الثانية. وعلى سبيل  تقول إنه عندما تسقط قنبلة من طائرة تتحرك بعد مضى عشر ثوان بسرعة قدرها :

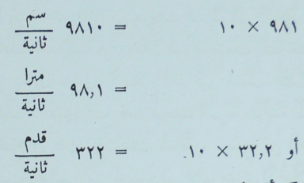
كما انها تكون قد قطعت مسافة قدرها:

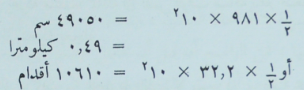
ومن بين إضافات غاليليو الهامة في مجال الديناميكا فكرة الحركة المركبة التي يمكن التعبير عنها بالمثال البسيط الآتي:

لنفرض أننا نمسك حجراً على ارتفاع خمس أقدام من سطح الأرض ثم تركناه يسقط، فتبعاً للقاعدة السابقة يصطدم الحجر بالأرض بعد مضى 0,96 ثانية، وذلك بطبيعة الحال لأن:

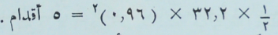
ولكن ماذا يحدث لو أننا عنا، إسقاط الحجر أعطيناه سرعة أفقية تساوي مثلاً، (10) أقدام في الثانية؟ إننا جميعاً نعرف من خبرتنا الشخصية أنه في مثل هذه الحالة يرسم الحجر مساراً منحنياً ليسقط على الأرض على بعد منا. ولكي نرسم هذا المسار يجب ان ندخل في الاعتبار ان للحجر حركتين : (1) حركة أفقية، يتحرك فيها بالسرعة المنتظمة التي اكسبناه إياها لحظة الإطلاق، (2) حركة رأسية نتيجة التساقط الحر يتحرك فيها بسرعة تتزايد بمضي الوقت.

ويمثل شكل (1-3) نتيجة إضافة الحركتين، حيث أخذنا على المحور ⁽⁴⁾ الأفقي مسافات متساوية تقابل المسافات التي يقطعها الحجر (أو الكرة) ، خلال الثانية الأولى، فالثانية الثانية، فالثالثة  . . . وهكذا . كما رسمنا على المحور الرأسي

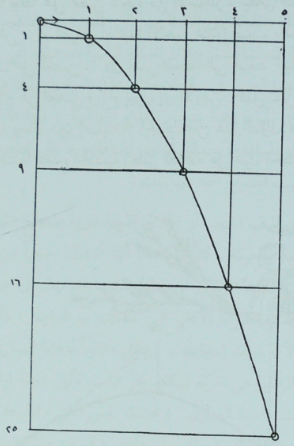
الشكل (1-3): إضافة (أو تركيب) حركة منتظمة في اتجاه أفق إلى حركة ذات عجلة في الاتجاه الرأسي يعرف المنحنى الناتج عن هذه الإضافة باسم القطع المكافئ.

مسافات تتزايد متناسبة مع مربعات الأعداد الصحيحة الكاملة تبعاً لقانون التساقط الحر. وتبين الدوائر الصغيرة الأوضاع الفعلية للكرة في أثناء سقوطها. وتقع هذه الدوائر على منحن هو القطع المكافئ. وإذا ما عمدنا إلى رمي الكرة بسرعة تبلغ قيمتها ضعف السرعة الأولى، وجدناها تقطع مسافة أفقية تعادل ضعف المسافة التي تقطعها في الحالة الأولى، بينما تظل حركتها الرأسية كما هي، وعلى ذلك تسقط على بعد من أقدامنا يعادل ضعف البعد الأول، ولكن الزمن الذي تستغرقه في الحالتين يظل واحد ولا يتغير. (لاحظ اننا في جميع هذه الحالات تهمل احتكاك الهواء، وهو عامل يؤدي إلى تحويل بسيط في مسار الكرة المقذوفة).

ومن التطبيقات الطريفة لنفس هذا المبدأ أو هذه القاعدة مسألة الغلامين اللذين يلعبان دور الخدمة العسكرية أو الحرب في الغابة ــ شكل (1-4) ــ .

ليكن غلام منهما وافقاً على غصن شجرة من الأشجار، ليطلق الثاني عليه رصاص بندقيته (الخرطوش. ثم لنفرض ان هذا الأخير عندما صوب بندقيته تماماً ومباشرة على الغلام الواقف على الغصن، وفي نفس اللحظة التي ضغط فيها زناد الندقية، انزلقت قدم الغلام عن الغصن وراح يهوى إلى الأرض. فهل تظن ان هذا السقوط إلى الأرض أنقذه وحال دون إصابته ؟ الجواب عن هذا السؤال هو بالنفي ! وهذا هو السر في أنه عندما تنعدم الجاذبية تنطلق القذيفة على طول الخط المستقيم ا ب جـ

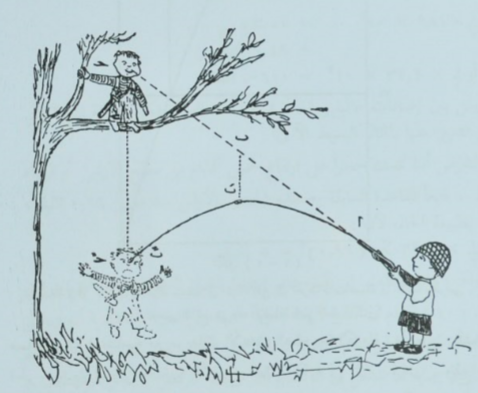
الشكل (1-4): لما كانت جميع الأجسام تتساقط بنفس العجلة، نجد انه إذا  أطلق غلام، يمثل لعبة حرب الغاية، قذيفة من بندقيته (الخرطوش) مباشرة على (العدو) الرابض فوق غصن الشجرة، فإن القذيفة تصيب أنف العدو إذا ما تعمد هذا السقوط لحظة الإطلاق.

الممتد إلى النقطة الأصلية التي كان يقف عليها الغلام. وعلى أية حال فإنه تحت تأثير الجاذبية (قبضة الأرض) تبدأ القذيفة في التساقط لحظة تركها فوهة البندقية، ونحصل بذلك على حركة مزدوجة : حركة منتظمة على امتداد الخط ا ب  جـ ، إلى جانب حركة اخرى ذات عجلة في الاتجاه الرأسي. ولكن لما كانت كل الأجسام المادية تتساقط بنفس العجلة فإن الحركتين الرأسيتين للقذيفة والصبي تتطابقات بحيث إنه عندما تصل القذيفة إلى النقطة ب التي تقع في منتصف المسافة إلى الهدف الأصل، تكون قد تساقطت خلال المسافة الرأسية ب ب ، التي تساوي تماماً المسافة ج ج التي يقطعها الصبي في سقوطه خلال تلك الفترة. وبدلا من أن تصل القذيفة ان النقطة جـ في نهاية المدة يفرض انعدام الجاذبية، نجدها في تلك اللحظة قد تساقطت خلال المسافة جـ ب التي تساوي جـ جـ التي قطعها الصبي في سقوطه. وعلى ذلك تصيب القذيفة أنفه دون شك.

وبدلاً من قذف الحجر أو إطلاق قذيفة نارية يستطيع المرء أن يكتفى بإسقاط جسم من مركبة متحركة. لنفرض مثلاً أننا أسقطنا حجراً من قمة صارى سفينة تدفعها الآلات بسرعة فائقة (أو سفينة تدفعها المجاديف في عهد غاليليو)، فإن الحجر يأخذ نفس السرعة الأفقية التي تنساب بها السفينة، ولذلك يستمر يتحرك بهذه السرعة الأفقية بعد إسقاطه ، ويظل ملازماً قاعدة الصارى. ولكن نظراً لأن حركة الحجر الرأسية هي حركة تساقط حر تحت تأثير عجلة الجاذبية، فإن الحجر يسقط تماماً عند قاعدة الصارى. ويحدث نفس الشيء بطبيعة الحال عندما تسقط جسماً داخل عربة قطار متحرك، أو داخل (قمرة) طائرة تحلق في الجو، مهما بلغت سرعة هذه المركبات.

وفي عصرنا هذا تبدو لنا هذه المسائل كلها بسيطة وواضحة، ولكن لم يكن الأمر كذلك في عهد غاليليو. ففي تلك الآونة ساد الاعتقاد ــ تبعاً لتعاليم أرسطو التي كانت تسيطر آنئذ على الفكر العلمي ــ بأن أي جسم لا يتحرك إلا إذا وقع تحت دفع قوة معينة، وأنه يركن إلى السكون بمجرد انقطاع عمل القوة المحركة.

وتبعاً لوجهة النظر هذه يهوى الحجر رأسياً إلى أسفل مباشرة بمجرد إسقاطه من قمة الصارى في نفس الوقت الذي تنساب فيه السفينة إلى الأمام (أي من غير يتأثر الحجر بحركتها ) ، ويكون من المنتظر ان يرتطم الحجر بسطحها قريباً من مؤخرتها. ومن خصائص مدارس العصور الوسطى أو سكولائيتها أن انفرد بمناقشة المسائل التي من هذا النوع المحترفون خلال مدة طويلة، فلم يهتم أحد مثلاً يتسلق صارى السفينة وهي تتحرك ليسقط من قمته حجراً !!

وتصور لنا فقرات الآتية من كتاب غاليليو (نقاش حول النظم الكبرى للعالم) الذي نشر عام 132 في فلورنسة، الموقف تصويراً واضحاً . وقد أقتفى غاليليو أثر كتاب قدماء الإغريق في إخراج كتابه على صورة حديث بين ثلاث أشخاص من فنيس مدينة العجائب: سالفياتس الذي يأخذ دور المؤلف نفسه، وساجر يدس وهو من العامة الأذكياء، وسمبليسيوس الذي لا يتوافر له الفهم الكافي لمدرسة أرسطوا التي يمثلها.

وهاك الحديث الذي دار بينهم حول حجر سقط من على صارى سفينة تنساب فوق اليم، ثم من أعلى برج شيد على أرض متحركة (كما يقول كبرنيق).

سالف : يقول أرسطو إن من بين القرائن المقنعة على ثبوت الأرض أن ترى القذائف التي تطلق أو ترمي رأسياً تقفل راجعة عمودياً، في نفس الخط الذي سارت عليه لتعود إلى نفس المكان الذا طلقت أو قذفت منه، وتسرى صحة هذه القاعدة مهما بلغ ارتفاع القذيفة. وعلى ذلك فمن الأوفق ان نرجع هنا إلى البينة المأخوذة عن قذيفة عندما تطلق رأسياً تماماً من مدفع (أو بندقية، وكذلك إلى غيرها من القراءن التي ساقها كل من ارسطو وبطليموس خاص بالأجسام الثقيلة التي عندما تسقط من أي ارتفاع يشاهد أنها تهبط خلال خطوط مستقيمة عمودية على سطح الارض. وإذا كان على أن ابداً بتوحيد هذه العقد فإني أطالب سميليسيوس بذلك، أما في حالة انكار أحدنا ما ذهب إليه بطليموس وأرسطو من ان الأجسام عندما تسقط حرة طليقة من على تنزل على خط مستقيم متعامد ⁽⁵⁾، أي يتجه مباشرة إلى المركز، فأي وسيلة يمكن ان يستخدمها لتدليل على ذلك؟

سمب: وسيلتنا إلى ذلك هي الحواس التي نتبين بها أن ذلك البرج أو غيره من المرتفعات يقف معتدلاً رأسياً ومتعامداً، ونرى ان ذلك الحجر ينزلق على الحائط دون ان ينحرف قدر سمك الشعرة إلى هذا الجانب أو ذلك، ويصل إلى الأرض تماماً تحت المكان الذي أسقط منه.

سالف: ولكن إذا حدث ان كانت الكرة الأرضية تلف وتدور، ومن ثم تحمل معها البرج كذلك، وأن الحجر كشط جانب البرج فعلاً وهو ينزلق عليه، فماذا يجب أن تكون حركته إذن؟

سمب : في هذه الحال ربما يكون من الأاوفق ان نتحدث عن حركته، غذ تكون له حركة يهبط بها من القسمة إلى القاعدة، كما تلزمه حركة اخرى يتابع بها مسار البرج المذكور.

سالف: وإذا يلزم أن تتركب إزاحته من حركتين ، ومن ثم ينتج ان الحجر لا يرسم ذلك الخط البسيط العمودي، ولكن خطأ مستعرضاً وربما لا يكون مستقيماً.

سمب : لا أستطيع ان أقول شيئاً من عدم استقامة، ولكني أعرف جيداً أنه من اللازم ان يكون المسار مستعرضاً.

سالف: أن ترى معي إذن أن مجرد رصد الحجر الساقط ومشاهدته ينزلق على طول البرج ليس معناه حتماً الجزم بأنه يرسم خطاً مستقيماً وعمودياً ما لم تفترض أولاً أن الأرض ثابتة لا تتحرك.

سمب: هذا حقيقي، لأنه لو كانت الأرض تتحرك لأصبح مسار الحجر مستعرضاً وليس متعامداً.

سالف: ويتمخض دفاع أرسطو  إن من بين القرائن المقنعة على ثبوت الأرض انر نرى القذائف التي تطلق أو ترمي رأسياً تقفل راجعة عمودياً، في نفس الخط الذي سارت عليه لتعود إلى نفس المكان الذي أطلقت أو قذفت منه، وتسري صحة هذه القاعدة مهما بلغ ارتفاع القذيفة. وعلى ذلك فمن الأوفق أن نرجع هنا إلى البينة المأخوذة عن قذيفة عندما تطلق رأسياً تماماً مدفع (او بندقية ، وكذلك إلى غيرها من تسقط من أي ارتفاع يشاهد أنها تهبط خلال خطوط مستقيمة عمودية على سطح الأرض. وإذا كان على أن أبدأ بتوحيد هذه العقد فإني أطالب سميليسيوس بذلك، أما في حالة انكار احدنا ما ذهب إليه بطلميوس وارسطو من ان الاجسام عندما تسقط حرة طليقة من على تنزل على خط مستقيم متعامداً ⁽⁶⁾، أي يتجه مباشرة إلى المركز، فأي وسيلة يمكن ان يستخدمها للتدليل على ذلك؟

سمب: وسيلتنا إلى ذلك هي الحواس التي نتبين بها ان ذلك البرج أو غيره من المرتفعات يقف معتدلاً رأسياً ومتعامداً، ونرى ان ذلك الحجر ينزلق على الحائط دون ان ينحرف قدر سمك الشعرة إلى هذا الجانب أو ذاك، ويصل إلى الأرض تماماً تحت المكان الذي أسقط منه.

سالف: ولكن إذا حدث ان كانت الكرة الارضية تلف وتدور، ومن ثم تحمل معها البرج كذلك، وأن الحجر كشط جانب البرج فعلاً وهو ينزلق عليه، فماذا يجب ان تكون حركته إذن؟

سمب : في هذه الحال ربما يكون من الأوفق ان نتحدث عن حركته ، إذ تكون له حركة يهبط بها من القمة إلى القاعدة، كما تلزمه حركة أخرى يتابع بها مسار البرج المذكور.

سالف: واذاً يلزم ان تتركب إزاحته من حركتين ، ومن ثم ينتج ان الحجر لا يرسم ذلك الخط البسيط العمودي، ولكن خطأ مستعرض وربما لا يكون مستقيماً.

سمب: لا أستطيع ان أقول شيئاً عن عدم استقامته، ولكني أعرف جيداً أنه من اللازم ان يكون المسار مستعرضاً.

سالف: انت ترى معي إذن ان مجرد رصد الحجر الساقط ومشاهدته ينزلق على طول البرج ليس معناه حتماً الجزء بأنه يرسم خطأ مستقيماً وعمودياً ما لم تفترض أولاً أن الأرض ثابتة لا تتحرك.

سمب: هذا حقيقي، لأنه لو كانت الأرض تتحرك الأصبح مسار الحجر مستعرضاً وليس متعامداً.

سالف: ويتمخض دفاع أرسطو إذاً عن استحالة، أو على الأقل عن اعتباره أمراً مستحيلاً ان يكتسب الحجر خليطاً من الحركة المستقيمة والحركة الدائرية، لأنه إذا لم يعتبر من المستحيلات إمكان تحرك الحجر في الحال تجاه المركز ومن حوله، كان عليه ان يدرك بداهة أن الحجر الساقط يجوز في أثناء هبوط أن يخدش البرج، سواء تحرك هذا أم لم يتحرك. وعلى ذلك فقط كان لا مناص من ألا يرى شيئاً يمكن أن يستنتج من هذا الخدش خاصاً بحركة الأرض أو سكونها . ولكن هذا لا يعني أرسطو بحال، فقد كان عليه ان يعبر عن هذه الفكرة لو أنها توافرت لديه، لأهميتها وضرورتها كجزء من دفاعه، وأيضاً لأنه لا يمكن التسليم بأن مثل تلك الظاهرة يعد أمراً مستحيلاً، او لأن أرسطو اعتبرها كذلك بالعقل. ولا داعي لتأكيد الأمر الأول، لأنني في سياق حديثي سوف أبين أنه ليس محتملاً فحسب بل هو ضروري كذلك. كما أنه لا لزوم لإثبات الثاني، لأن أرسطو نفسه يفترض أن النار تسري بحسب الطبيعة في خط مستقيم، كما تسري  من حولها مع الدورة اليومية التي تسبغها السموات على عنصر النار كله وأغلب أجزاء الهواء العلوي. فلو أنه اعتبر من الممكن خلط الحركة المستقيمة إلى أعلى مع الحركة الدائرية التي تسبغ على النار والهواء من تجويف كرة، القمر لهان عليه أمر إمكان خلط حركة الحجر المستقيمة إلى أسفل مع حركته الدائرية التي نفترضها شيئاً طبيعياً لكل الكرة الأرضية ، التي يكون الحجر جزءاً منها.

ونجد بعد ذلك في "كتاب الحوار" أن سالفياتس يقترح إجراء تجربة مثيرة ليدلل بها على وجهة نظرة التي أوضحتها في نقاشه السابق.

سالف: وإذا لم أكن مخطئاً، فإن إثارتك الشك حول هذا الأمر اكثر من غيره إنما يتوقف على ما أمدت به الطيور بما يكفل لها استخدام قواها حسيماً أرادت ضد الحركة الابتدائية للأجسام الأرضية. فمثلاً نحن نراها تطير إلى أعلى وهو امر يلزم ان يكون مستحيلاً تماماً على الأجسام الثقيلة، على حين أنها عندما تموت لا تستطيع إلا السقوط إلى أسفل، وعلى ذلك يمكننا ان نتبين ان القواعد التي تنطبق على جميع القذائف المذكورة سابقاً لا يمكن أنطباقها على الطيور. ولما كان هذا الأمر مما لا شك فيه فإننا نرى الطيور الحية تتصرف بطريقة تختلف عن الأجسام عندما تهوى إلى الأرض  فإذا ما أسقطنا من قمة برج يفعله الحجر، أي إنه سوف يتبع أولاً الحركة اليومية العامة، وبعد ذلك حركة الهبوط تماماً مثل الحجر. اما إذا كان الطائر حياً عند إسقاطه فما الذي يمنعه (مع بقاء الحركة اليومية فيه إلى النهاية) من الحركة بمساعدة جناحيه ليقصد أي نقطة يرغبها في الأفق؟ ولما كانت هذه الحركة الجديدة مقصورة على الطيور ونحن لا نشاركها فيها، فإنه لا مناص لنا من رصدها ومشاهدتها . ويحمل القول أنه لا يختلف طيران الطير عن إطلاق القذائف تتحرك بمؤثرات خارجية، بينما تحلق الطيور تبعاً لمبدأ داخل. ولكن نعطى برهاناً أخيراً على عدم إيجابية كل التجارب التي من قبل، أرى ان الوقت قد حان والمكان يصلح لعرض وسيلة  تبين بها كيف تعمل محاولة صادقة لها جميعاً.

أقفل عليك مع صديق لك باب أكبر غرفة تحت سطح سفينة كبيرة ومعكما عدد من البعوث والذباب وغيرها من الكائنات الصغيرة ذات الأجنحة، بعد ان تكون قد احضرت معك إناء كبير به ملاء بداخلة بعض الأسماك، وعلقت زجاجة في السقف يقطر منها الماء نقطة نقطة متساقطاً داخل فوهة ضيقة لزجاجة اخرى موضوعة تحتها. بعد ذلك لاحظ ، والسفينة ساكنة لا تتحرك، كيف تطير تلك الحيوانات الصغيرة المجنحة بسرعة متجانسة تجاه كافة أرجاء الغرفة، وكيف تعوم الأسماك دون تمييز بين جوانب الإناء ، وكيف تتساقط جميع النقاط التي تقطر من الزجاجة العليا داخل الزجاجة السفلى. وإذا ما أردت أي شيء من صديقك فإنه لا يحتاج لكي يدفعه إليك غلى قوة أكبر في أتجاه او آخر ما دامت المسافات متساوية ، وعندما تعمد إلى القفز بكل قواك تجد ان المسافة التي تقطعها تظل ثابتة إلى أي جهة ترغبها . وبعد ملاحظة كل هذه الدقئق، ورغم أنه لا ينكر أحد أن الأمور تجري على هذا النحو ما دامت السفينة ساكنة، أجعل السفينة تتحرك بأي سرعة تعجبك بشرط أن تظل الحركة منتظمة من غير ذبذبة هنا أو هناك ، تجد أنه يستحيل عليك تمييز أي تغير يطرأ على الظواهر السابق ذكرها، كما أنه لا يمكنك أن تحكم عن طريقة أية ظاهرة منها ما إذا كانت السفينة تتحرك أولاً تتحرك بتاتاً، وعلة ذلك ان حركة السفينة يعتادها كل ما فيها ويعتادها الهواء كذلك، أعني لو أن الغرفة أغلقت على هذه الأشياء. اما إذا كانت فوق سطح السفينة في الهواء الطلق ولم تجبر على ملازمة السفينة، فإنه ينجم عن ذلك ملاحظة بعض الفروق تطرأ على الدخان وعلى ملازمة السفينة، فإنه ينجم عن ذلك ملاحظة بعض الفروق تطرأ على الدخان وعلى جانب من تلك الظواهر. وليس من شك ان الدخان يتخلف على قدر الهواء نفسه. والذباب كذلك والبعوض يعوقه الهواء ولن يتمكن من متابعة حركة السفينة إذا ما فصل عنها بأي مسافة، إلا أنه يظل قريباً منها، لأن السفينة بحكم انها تركيب غير قابل للتجزئة ، تحمل معها جانباً من أقرب هواء لها، وذلك تتبع هذه الأشياء السفينة دون أي مشقة او صعوبة. ولنفس هذا السبب نرى أحياناً في مراكز ركوب الخيل أن ذباب الخيل المضنى يتبعها، فيحط تارة على جزء من جسمها ثم يطير إلى جزء آخر تارة اخرى. أما في حالة النقط المتساقطة فإن الفرق يكون طفيفاً جداً يكاد لا يدرك، وكذلك الحال مع قفزات الأجسام الوثيدة المتزنة.

ساجر: رغم أنه لم يخطر ببالي أن أجري مثل هذه المشاهدات عندما كنت في البحر ، إلا أنني واثق من أنها صادقة على النحو الذي وصفته. وتأكيداً لذلك أتذكر أنني عندما كنت في (قمرتي) تساءلت مائة مرة عما إذا كانت السفينة تتحرك أو واقفة في مكانها، وكنت أحياناً أتصورها تتحرك في اتجاه معين في الوقت الذي كانت تنساب فيه في الاتجاه المضاد. وعلى ذلك فإنني راض تماماً ومقتنع بعدم صلاحية جميع تلك التجارب التي أثبتت العكس.

والآن يبقى الاعتراض القائم على ما تثبته لنا الحبرة وتدل عليه، وهو ان حركة الدوران السريعة لها فعل الطرد والتشتيت للمواد الملتصقة بآلة الدوران. وقد بنى الكثيرون، ومنهم بطليموس ، على هذه الحقيقة فكرة أنه إذا كان من الضروري أن تدور الأرض ويتلف بمثل تلك السرعة العظيمة، وجب ان يندفع كل ما على سطحها من حجارة وكائنات إلى السماء، ولن تكون هناك مادة بناء تبلغ من القوة ما يتيح لنا فرصة تثبيت المباني في أساسها، فتلقى نفس المصير.

وفي عصرنا هذا تعرف العبارة القائلة بأنه يستحيل التحقق من أن السفينة راسية أو تنساب عبر البحر عن طريق إجراء أي تجربة ميكانيكية في داخل (قمرة) مقفلة باسم "مبدأ النسبية لغاليليو"، ولقد مرت قرون ثلاثة تطور خلالها علم الفيزياء حتى ظهر ألبرت أنشتين فعمم هذا المبدأ عندما نرصد الظواهر الضوئية والكهرومغناطيسية في مكان مقفل يسير بسرعة منتظمة . ولقد وقفت إضافات غاليليو في ميدان علم الميكانيكا عند هذا الحد.

ـــــــــــــــــــــــــــــــــــــــــ

(1) قبضة الأرض . (المترجم).

(2) عندما نعبر عن ذلك جبرياً نقول: إذا كانت المسافة الكلية المقطوعة في نهاية الزمن  ن هي ن2، تكو المسافة المقطوعة خلال الفترة الأخيرة هي:

ن2- (ن-1)2 = 2ن-1                  (المؤلف).

(3) بإذن من كتاب غاليليو غاليل : (حوار حول النظم الكبرى للعالم) مطبعة جامعة شيكاغو عام 1953 . من ص244 إلى ص245 . (المؤلف).

(4) يعرف مثل هذا الشكل بالتمثيل  أو الرسم البياني، حيث يرسم محوران متعامدان أحدهما أفق يقال له في العادة محور السينات، والثاني رأس هو محور الصادات. ويقسم كل محور بحيث يمكن أخذ قيم أي كمية متغيرة عليه، ومن ثم تحديد نقطة على الشكل تقابل قراءتين أو قيمتين مختلفتين لمتغيرين مأخوذين على المحورين. (المترجم).

(5) على سطح الأرض (المترجم).

(6) على سطح الأرض (المترجم).