For three vectors a, b, and c the vector triple product is defined a ˄ (b ˄ c). The brackets are important because a ˄ (b ˄ c) ≠ (a ˄ b) ˄ c. In fact, it can be demonstrated that

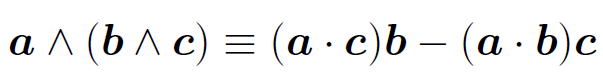    (1.1)

and

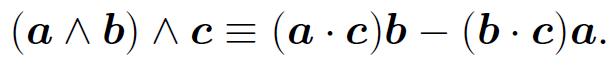 (1.2)

Let us try to prove the first of the above theorems. The left-hand side and the right-hand side are both proper vectors, so if we can prove this result in one particular coordinate system then it must be true in general. Let us take convenient axes such that the x-axis lies along b, and c lies in the x-y plane. It follows that b = (b_x, 0, 0), c = (c_x, c_y, 0), and a = (a_x, a_y, a_z). The vector b ˄ c is directed along the z-axis: b ˄ c = (0, 0, b_xc_y). It follows that a ˄ (b ˄ c) lies in the x-y plane: a ˄ (b ˄ c) = (a_xb_xc_y;-a_xb_xc_y, 0). This is the left-hand side of Eq. (1.1) in our convenient axes. To evaluate the right-hand side we need a . c = a_xc_x + a_yc_y and a . b = a_xb_x. It follows that the right-hand side is

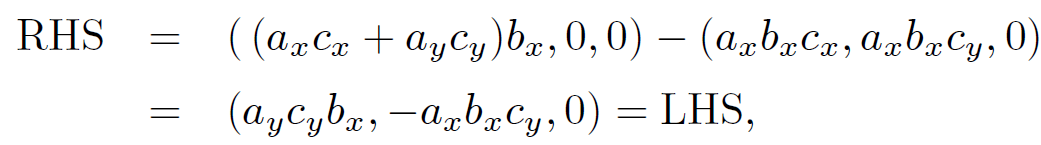 (1.3)

which proves the theorem.