
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The classical image problem
المؤلف:
Richard Fitzpatrick
المصدر:
Classical Electromagnetism
الجزء والصفحة:
p 172
4-1-2017
2945
The classical image problem
So, how do we actually solve Poisson's equation,
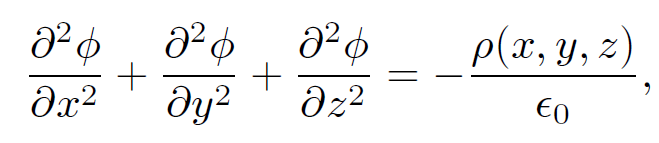 (1.1)
(1.1)
in practice? In general, the answer is that we use a computer. However, there are a few situations, possessing a high degree of symmetry, where it is possible to find analytic solutions. Let us discuss some of these solutions. Suppose that we have a point charge q held a distance d from an infinite, grounded, conducting plate. Let the plate lie in the x-y plane and suppose that the point charge is located at coordinates (0, 0, d). What is the scalar potential above the plane? This is not a simple question because the point charge induces surface charges on the plate, and we do not know how these are distributed. What do we know in this problem? We know that the conducting plate is an equipotential. In fact, the potential of the plate is zero, since it is grounded. We also know that the potential at infinity is zero (this is our usual boundary condition for the scalar potential). Thus, we need to solve Poisson's equation in the region z > 0, for a single point charge q at position (0, 0, d), subject to the boundary conditions
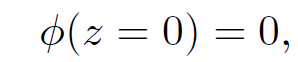 (1.2)
(1.2)
and
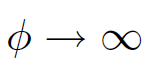 (1.3)
(1.3)
as x2 + y2 + z2 → ∞. Let us forget about the real problem, for a minute, and concentrate on a slightly different one. We refer to this as the analogue problem. In the analogue problem we have a charge q located at (0, 0, d) and a charge –q located at (0, 0, -d) with no conductors present. We can easily find the scalar potential for this problem, since we know where all the charges are located. We get
 (1.4)
(1.4)
Note, however, that
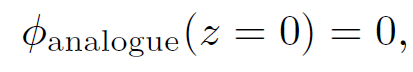 (1.5)
(1.5)
and
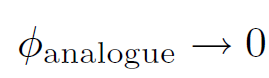 (1.6)
(1.6)
as x2 + y2 + z2 → ∞. In addition, ϕanalogue satisfies Poisson's equation for a charge at (0, 0, d), in the region z > 0. Thus, ϕanalogue is a solution to the problem posed earlier, in the region z > 0. Now, the uniqueness theorem tells us that there is only one solution to Poisson's equation which satisfies a given, well-posed set of boundary conditions. So, ϕanalogue must be the correct potential in the region z > 0. Of course, ϕanalogue is completely wrong in the region z < 0. We know this because the grounded plate shields the region z < 0 from the point charge, so that ϕ = 0 in this region. Note that we are leaning pretty heavily on the uniqueness theorem here! Without this theorem, it would be hard to convince a skeptical person that ϕ = ϕanalogue is the correct solution in the region z > 0. Now that we know the potential in the region z > 0, we can easily work out the distribution of charges induced on the conducting plate. We already know that the relation between the electric field immediately above a conducting surface and the density of charge on the surface is
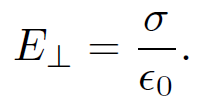 (1.7)
(1.7)
In this case,
 (1.8)
(1.8)
so
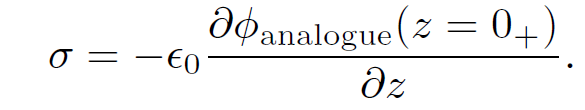 (1.9)
(1.9)
It follows from Eq. (1.4) that
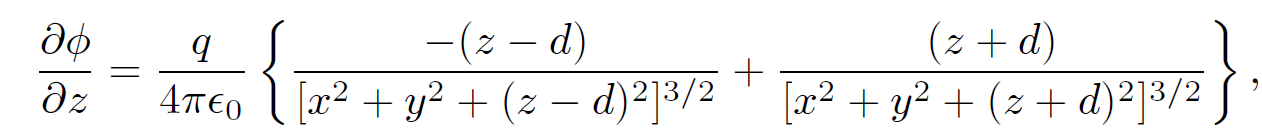 (1.10)
(1.10)
so
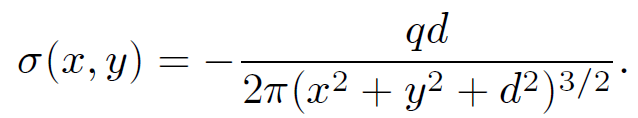 (1.11)
(1.11)
Clearly, the charge induced on the plate has the opposite sign to the point charge. The charge density on the plate is also symmetric about the z-axis, and is largest where the plate is closest to the point charge. The total charge induced on the plate is
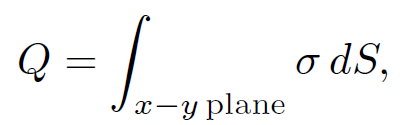 (1.12)
(1.12)
which yields
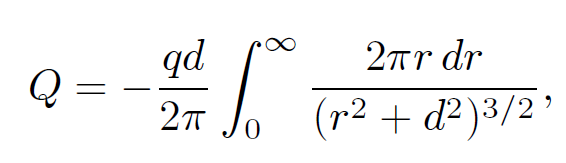 (1.13)
(1.13)
where r2 = x2 + y2. Thus,
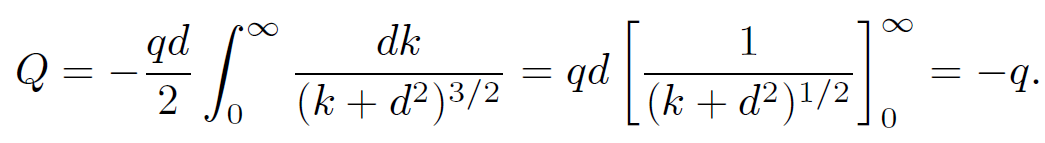 (1.14)
(1.14)
So, the total charge induced on the plate is equal and opposite to the point charge which induces it. Our point charge induces charges of the opposite sign on the conducting plate. This, presumably, gives rise to a force of attraction between the charge and the plate. What is this force? Well, since the potential, and, hence, the electric field, in the vicinity of the point charge is the same as in the analogue problem then the force on the charge must be the same as well. In the analogue problem there are two charges ±q a net distance 2d apart. The force on the charge at position (0, 0, d) (i.e., the real charge) is
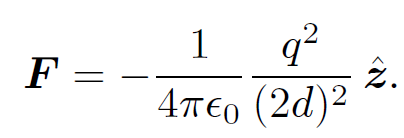 (1.15)
(1.15)
What, finally, is the potential energy of the system. For the analogue problem this is just
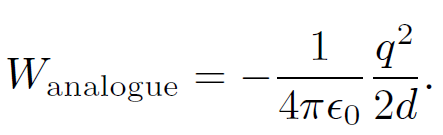 (1.16)
(1.16)
Note that the fields on opposite sides of the conducting plate are mirror images of one another in the analogue problem. So are the charges (apart from the change in sign). This is why the technique of replacing conducting surfaces by imaginary charges is called ''the method of images". We know that the potential energy of a set of charges is equivalent to the energy stored in the electric field. Thus,
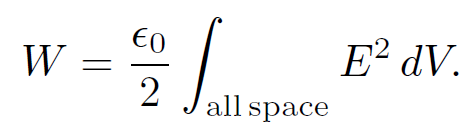 (1.17)
(1.17)
In the analogue problem the fields on either side of the x-y plane are mirror images of one another, so E2(x, y, z) = E2(x, y,-z). It follows that
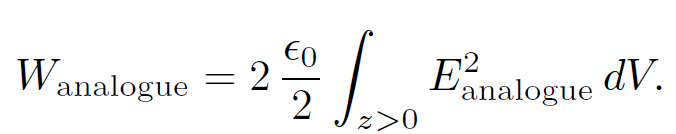 (1.18)
(1.18)
In the real problem
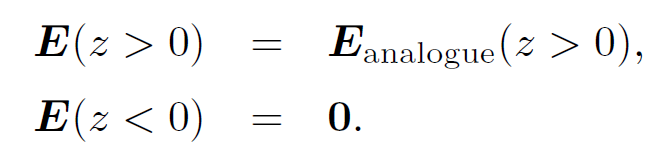 (1.19)
(1.19)
So,
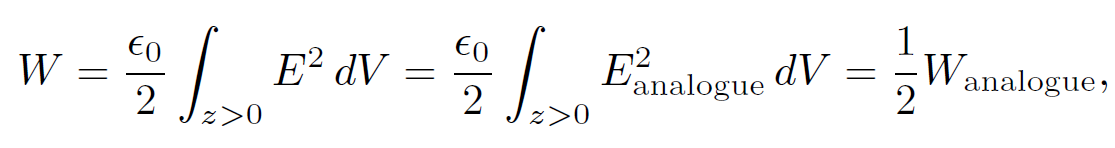 (1.20)
(1.20)
giving
 (1.21)
(1.21)
There is another method by which we can obtain the above result. Suppose that the charge is gradually moved towards the plate along the z-axis from infinity until it reaches position (0, 0, d). How much work is required to achieve this? We know that the force of attraction acting on the charge is
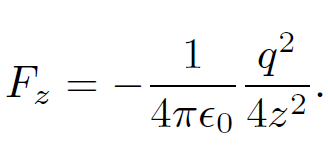 (1.22)
(1.22)
Thus, the work required to move this charge by dz is
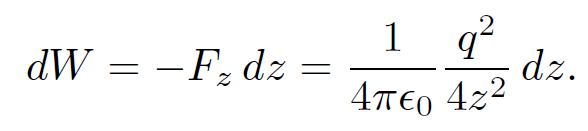 (1.23)
(1.23)
The total work needed to move the charge from z = ∞ to z = d is
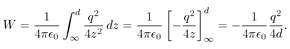 (1.24)
(1.24)
Of course, this work is equivalent to the potential energy we evaluated earlier, and is, in turn, the same as the energy contained in the electric field. There are many different image problems, each of which involves replacing a conductor (e.g., a sphere) with an imaginary charge (or charges) which mimics the electric field in some region (but not everywhere). Unfortunately, we do not have time to discuss any more of these problems.
 الاكثر قراءة في الكهربائية
الاكثر قراءة في الكهربائية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















