
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Force Law for SHM
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 178
30-12-2016
2873
Force Law for SHM
Now consider Newton's law for a Spring where the force is given by F = -kx (Hooke's law), where k is called the spring constant. Substituting into
F = ma
-kx = ma
but we found that  giving
giving
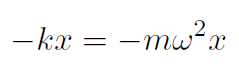
or
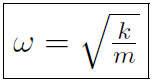
which is the angular frequency for an oscillating spring. The period is obtained from  or
or
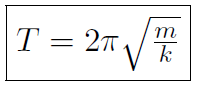
Notice an amazing thing. The period does not depend on the amplitude of oscillation xm! When a spring is oscillating, the oscillations tend to die down in amplitude xm but the period of oscillation remains the same! This is crucial to the operation of clocks. I can ''wind" my spring clock by just pulling on it a bit and still the period is the same.
Navigation and Clocks
NNN - FIX For a pendulum, this independence of the period on the amplitude was first noticed by Galileo and led to the development of clocks which was very important for navigation. The reason was that it enabled one to determine longitude on Earth. (Latitude was easy to determine just by measuring the height of the Sun in the sky at noon.) By dragging knotted ropes behind a ship it was easy to measure the speed of a ship. If one knew how long one had been travelling (i.e. measure the time of travel, say with a pendulum or spring clock) then one knew the distance from the port from which one had set sail. Knowing longitude and latitude gives one's position on the Earth. Thus the invention of accurate clocks (based on the independence of period and amplitude) enabled accurate estimates of longitude and thus revolutionized navigation.
Example F = ma is really a differential equation, that is an equation involving derivatives. For the spring, it becomes 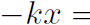
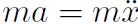 where
where 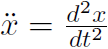 . Thus the differential equation is
. Thus the differential equation is

In mathematics there are special techniques for solving differential equations, which you will learn about in a special differential equations course. Using these special techniques one can prove that x = xm cos  t is a solution to the above differential equation. (Just like the solution to the algebraic equation x2 - 5 = 4 is x = ±3. We verify this solution by sustituting, (±3)2 -5 = 9-5 = 4). Many students will not have yet learned how to solve differential equations, but we can verify that the solution given is correct. Verify that x = xm cos
t is a solution to the above differential equation. (Just like the solution to the algebraic equation x2 - 5 = 4 is x = ±3. We verify this solution by sustituting, (±3)2 -5 = 9-5 = 4). Many students will not have yet learned how to solve differential equations, but we can verify that the solution given is correct. Verify that x = xm cos  t is a solution to the differential equation
t is a solution to the differential equation
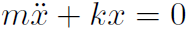
Solution
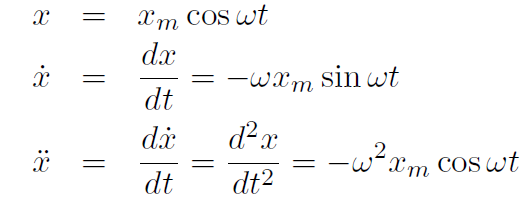
Substitute into
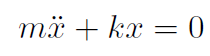
giving
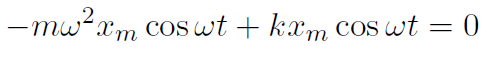
or
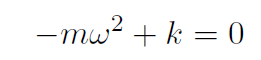
Thus if

then x = xm cos 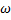 t is a solution.
t is a solution.
Example When a mass is suspended from the end of a massless spring, the spring stretches by a distance x. If the spring and mass are then put into oscillation, what is the period ?
Solution We saw that the period is given by 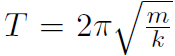 . We don't know m or k ! We can get k from Hooke's law F = -kx. The weight W = mg stretches the spring, thus mg = kx or
. We don't know m or k ! We can get k from Hooke's law F = -kx. The weight W = mg stretches the spring, thus mg = kx or  . Thus
. Thus
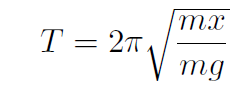
and fortunately m cancels out giving

 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















