
 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 16-3-2016
Date: 26-12-2016
Date: 24-3-2016
|
The photon model of a single mode laser
Let us consider a single kind of photons whose number we shall denote by n. Because in the following we are interested in the genuine laser process we shall neglect the spontaneous emission rate WN2. We shall see later anyway that the stimulated emission rate (N2 – N1) Wn plays quite a different role than the rate WN2. This becomes manifest in the statistical properties of laser light which we can treat only later, however. Therefore we start from the following equation for the temporal change of the photon number:
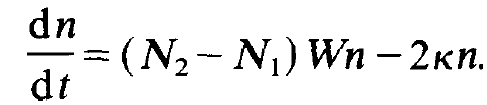 (1.1)
(1.1)
Due to the laser process not only the photon number changes but also the occupation numbers of the atoms change. Let us consider for simplicity
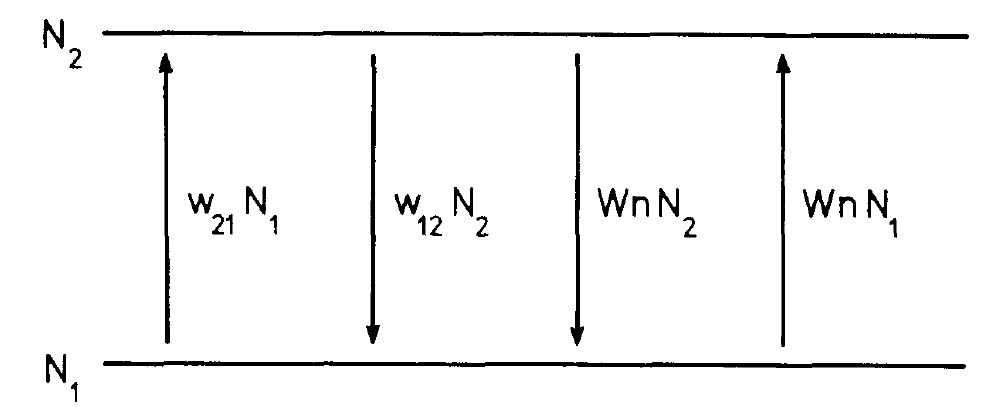
Fig. 1.1. The various optical transitions in a system of two-level atoms with the occupation numbers N1 and N2.
a system of two-level atoms, and let us study the temporal change of the occupation numbers N1 and N2. The number N2 increases by the excitation of electrons by the pumping process. The transition rate is proportional to the number of electrons available in the ground states of the individual atoms, i.e. it is proportional to N1. The corresponding proportionality factor will be denoted by w21 (fig. 1.1). Here and in the following we have to note that we must read the indices of the w's from right to left, i.e. w21 refers to the transition from level 1 to level 2. This transition rate depends, of course, on the optical properties of the atoms or, more precisely speaking, on the corresponding optical transition matrix elements. Finally w21 is proportional to the intensity of the pump light. We shall not discuss this in detail but we shall rather consider w21 as a "control parameter" which we can manipulate from the outside. Atoms being in level 2 can make transitions into the ground state by means of radiationless transitions in which no photons are emitted. Such processes can be caused, for instance, by collisions in gases or by the interaction between atoms with lattice vibrations in solids. The rate of these transitions is, of course, proportional to the number of excited atoms, N2. The corresponding proportionality factor will be denoted by w12. By means of this description we also take care of radiative processes which do not belong to the emission of the kind of photons under consideration here. Finally the processes of stimulated emission and absorption take place. The number of transitions per second is given by (N2- N1) Wn. Collecting all the contributions just mentioned we obtain the rate equation for the occupation number of level 2,
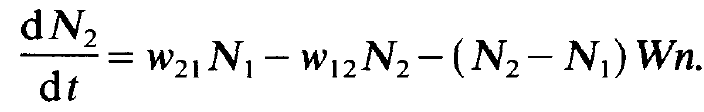 (1.2)
(1.2)
Level 1 can be treated in a completely analogous fashion. We then obtain
 (1.3)
(1.3)
Adding the eqs. (1.2) and (1.3) results in
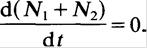 (1.4)
(1.4)
This means that the total occupation number of levels 1 and 2 remains constant. It is equal to the total number of all laser atoms
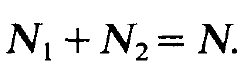 (1.5)
(1.5)
Because eqs. (1.1) to (1.3) contain the difference of the occupation numbers or, in other words, the inversion N2- N1, we introduce this quantity as a new variable
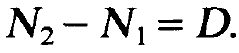 (1.6)
(1.6)
On the other hand N1 and N2 can be expressed by means of N and D,
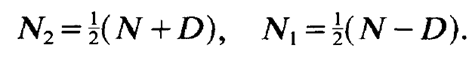 (1.7)
(1.7)
Because N is a constant we have to deal with a single variable D only. Therefore it suggests itself to express eqs. (1.1)-(1.3) by means of that variable. Subtracting (1.3) from (1.2) and using (1.7) yields
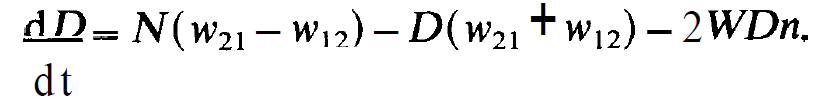 (1.8)
(1.8)
This equation can be brought into a form which lets transpire its physical meaning still more when we remember that the w's have the meaning of transition rates, i.e. that they are inversely proportional to certain transition times. Therefore we introduce a time constant T by the relation
 (1.9)
(1.9)
Furthermore we study which inversion D = D0 will result if only pump and relaxation processes occur but no laser process. We obtain that quantity by putting the 1.h.s. of (1.8) = 0 and by omitting the last term in (1.8). We then readily obtain
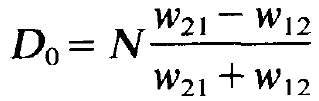 (1.10)
(1.10)
For reasons which we shall explain below, this inversion is called the unsaturated inversion. Inserting Do and (1.9) in (1.8) we finally obtain
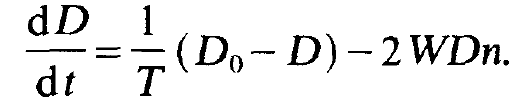 (1.11)
(1.11)
When we neglect for the moment being the last term in (1.1l), we can readily solve this differential equation and find a solution which tells us that D relaxes towards the value Do within the time T (compare the exercise). By use of (1.6) we can write the rate equations of the photons in the form
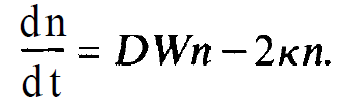 (1.12)
(1.12)
Eqs. (1.11) and (1.12) are the fundamental laser equations which we shall discuss in more detail. Because the r.h.s. of these equations contain products of the variables D and n, these equations are nonlinear and in general cannot be solved in closed form. Therefore we shall proceed from the simple case to more complicated cases when discussing and solving these equations. In the most simple case n and D are time independent, i.e. we consider the stationary state.
Stationary solution. In this case we have
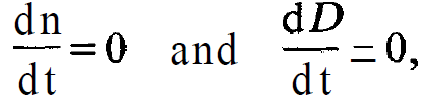 (1.13)
(1.13)
so that (1.11) reduces to
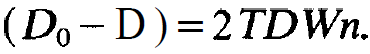 (1.14)
(1.14)
Solving this equation with respect to the inversion D we obtain
 (1.15)
(1.15)
Eq. (1.15) teaches us that the actual inversion D decreases from the inversion D0, which is prescribed by pump and relaxation processes only, when the photon number increases. This fact is expressed in technical terms by saying that a saturation of the inversion occurs. This effect can most easily be represented when the photon number n is still small. In this case we replace (1.15) by the relation
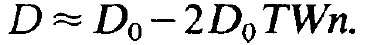 (1.16)
(1.16)
As noted above, D0 is the unsaturated inversion. The term containing n is called saturation. Inserting (1.15) in (1.12) and using dn/dt = 0 we obtain after a slight transformation
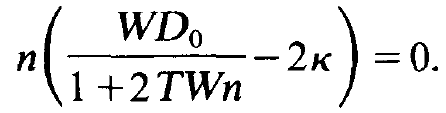 (1.17)
(1.17)
This equation possesses the two solutions
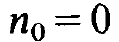 (1.18)
(1.18)
and
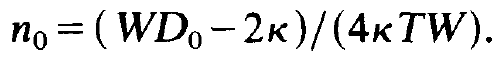 (1.19)
(1.19)
(Because n is a stationary solution we have supplied n with the index 0.) n0= 0 means that no photons are produced, i.e. that no laser action takes place. Therefore let us consider (1.19) and in particular the first factor on the r.h.s., ( WD0- 2k) . If we pump the laser only weakly, D0 is small so that
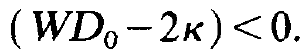 (1.20)
(1.20)
But because the photon number must not be negative, (1.19) is eliminated as a possible solution and only (1.18) remains. Therefore no laser action takes place. If we increase D0 such that
 (1.21)
(1.21)
holds, the solution (1.19) with n0> 0 becomes possible and we obtain laser action. It is a simple matter to convince oneself that (1.21) is identical with the laser (compare exercise). The increase of no with increasing Do is represented in fig. 1.2. While below the critical value D0= 2k/W there is no laser action, it occurs above that value and no increases rapidly. These considerations do not explain why we can exclude the solution n0 = 0 in the region (1.21). To this end we have to consider the time dependent equations. Our result that below laser threshold no photons are present at all stems from our neglect of spontaneous emission. We can take that effect into account only much later when we consider in chapter 10 the quantum theory of the laser. Approximate time dependent solutions Because the time dependent equations cannot be solved in closed form we shall try to solve them approximately. To this end we make two

Fig. 1.2. Emitted photon number no versus unsaturated inversion Do. In this model, below the critical inversion D0 = 2k/W no laser emission takes place. Beyond that inversion the photon number increases linearly.
assumptions. Let us consider the deviation of D from the unsaturated inversion D0, i.e. D – D0. Let us assume that D – D0 changes only little over times T (compare exercises). Expressed mathematically this means that
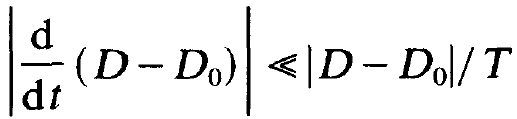 (1.22)
(1.22)
shall hold. Because Do is time independent, i.e. dD0/dt = 0, we may neglect the 1.h.s. of (1.1l), i.e. dD/dt compared to (D0- D)/T which occurs on the r.h.s. or, in other words, we may put dD/dt = 0 in eq. (1.1I). This allows us to solve (1.11) immediately by expressing D(t) by means of the instantaneous value of n(t) as we did in (1.15) above. But in contrast to that former result n and D now depend on time t. Inserting (1.16) in (1.12) and slightly rearranging the terms we obtain the laser equation
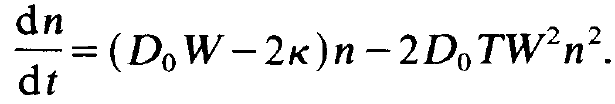 (1.23)
(1.23)
This equation can be interpreted as follows. When the laser is pumped only weakly the inversion D0 is small or even negative. In this case we have (D0W – 2k)< 0 and the total r.h.s. of (1.23) is negative, i.e. dn/dt is negative. Even if at an initial time some photons are present, for instance by spontaneous emission, the photon number decreases exponentially. If we increase the pump strength we finally obtain (Do W - 2K) > 0. Because usually in the beginning of the laser process the photon number n can be assumed small we may first neglect the quadratic term in n in (1.23) compared to the linear term. In this case an exponential increase of the photon number happens according to (1.23). In other words we have to deal with an "instability". Spontaneously produced photons are multiplied by the process of stimulated emission like an avalanche. Of course, the photon number does not increase exponentially for ever because finally the term quadratic in (1.23) becomes influential and lets the r.h.s. of (1.23) tend to 0. This implies that dn/dt tends to 0 and eventually the stationary state n = n0 will be reached. The quadratic term stems from the saturation of the inversion as can be easily derived from (1.16). The saturation makes it possible that a stationary state is reached. If we start with a photon number n which is bigger than that of the stationary state, n0, the second term in (1.23) dominates. In this case the r.h.s. is negative and consequently the photon number decreases and eventually acquires the stationary value, no. These results are represented in figs. 1.3a and 1.3b. The explicit time dependent solution of eq. (1.23) is derived in exercise 3 of this section.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|