Applying Newton Laws
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p69
15-12-2016
2976
Applying Newton's Laws
Example A chandelier of mass m is hanging from a single cord in the ceiling. Derive a formula for the tension in the cord. If m = 50 kg evaluate a numerical answer for the tension.
Solution Carefully draw a diagram showing all forces, as seen in Fig. 1.1. Then solve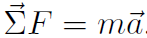 
. Thus
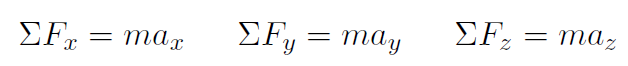
but all forces and acceleration in the x and z directions are zero and so the only interesting equation is
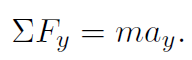
Now the forces are tension (+T) in the up direction and weight (-W) in the down direction. You don't want the chandelier to move, so ay = 0. Thus
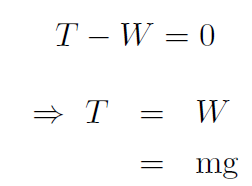
which is the formula we seek. Putting in numbers:
T = 50kg× 9.8 m/sec2 = 490 kg m/sec2 = 490 N
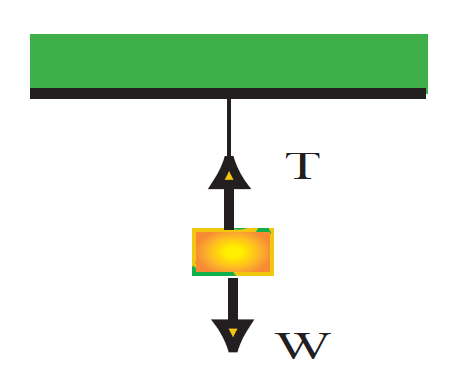
FIGURE 1.1 Chandelier hanging from ceiling.
Example A chandelier of mass m is now suspended by two cords, one at an angle of α to the ceiling and the other at θ. Derive a formula for is the tension in each cord. If m = 50kg and α = 60o and θ = 30o evaluate a numerical answer for each tension.
Solution Again carefully draw a figure showing all forces. See Fig. 1.2.
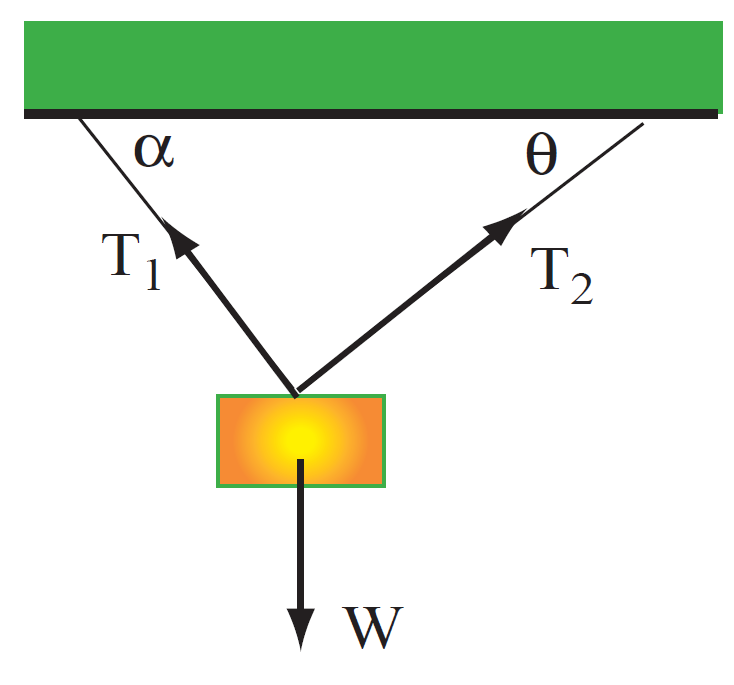
FIGURE 1.2 Chandelier suspended by 2 cables. In the z direction all forces and acceleration are zero. We need to consider the x and y directions (both with ax = ay = 0), namely,
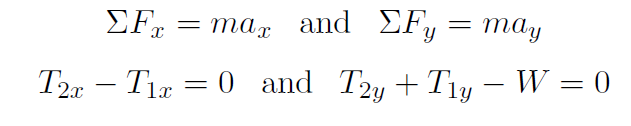
Now
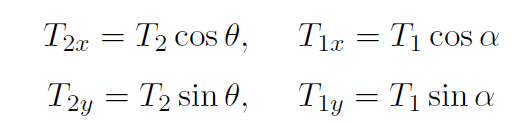
giving
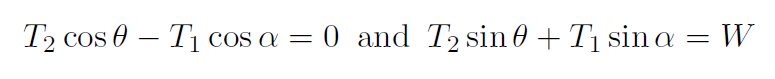
The x equation gives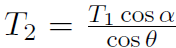 
which is substituted into the y equation giving
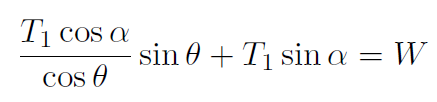
or
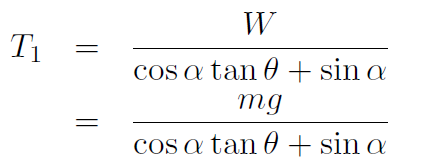
and upon substitution
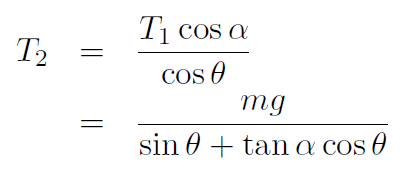
which are the formulas we seek. Putting in numbers gives:
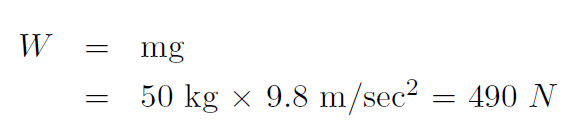
Thus
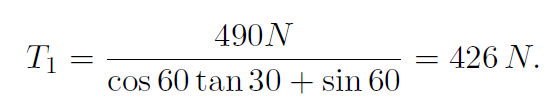
Now put back into
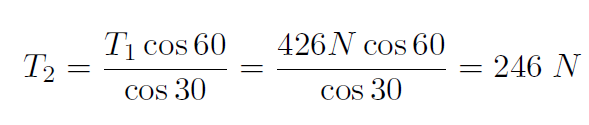
Example If you normally have a weight of W, how much will a weight scale read if you are standing on it in an elevator moving up at an acceleration of a ?
Solution The reading on the scale will just be the Normal force.
Thus
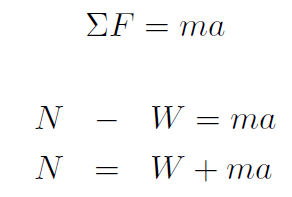
The answer makes sense. You would expect the scale to read a higher value.
Example A block of mass m slides down a frictionless incline of angle θ.
A) What is the normal force?
B) What is the acceleration of the block?
Solution In Fig. 1.3 the forces are drawn. Notice that I have chosen the orientation of the y axis to lie along the normal force. You could make other choices, but this will make things easier to work out.
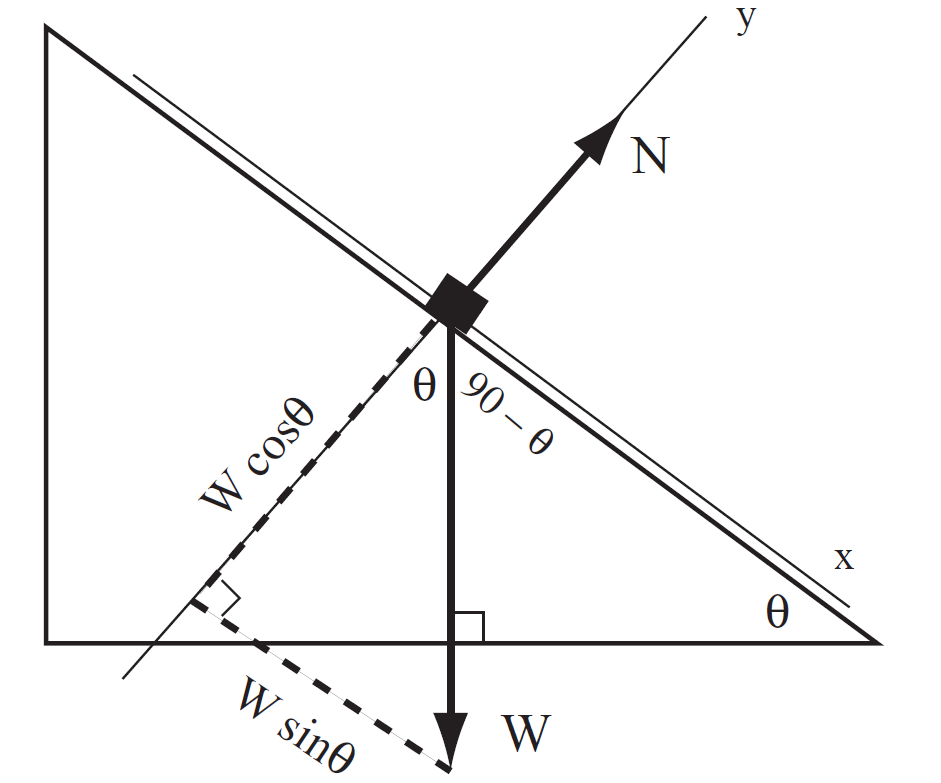
FIGURE 1.3 Block sliding down frictionless incline.
A) Analyzing the y direction,
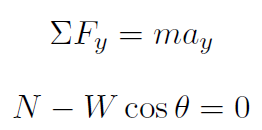
because the block has zero acceleration in the y direction.
Thus
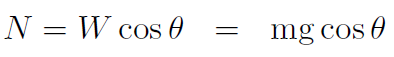
B) Analyzing the x direction,
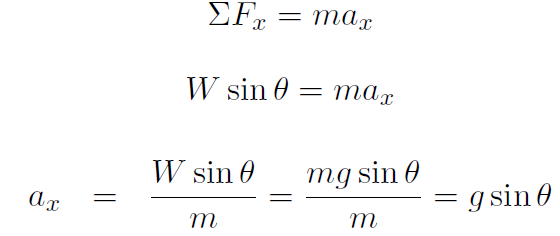
Example Derive a formula for the acceleration of the block system shown in Fig. 1.4 (Atwood machine). Assume the pulley is frictionless and the tension T is the same throughout the rope.
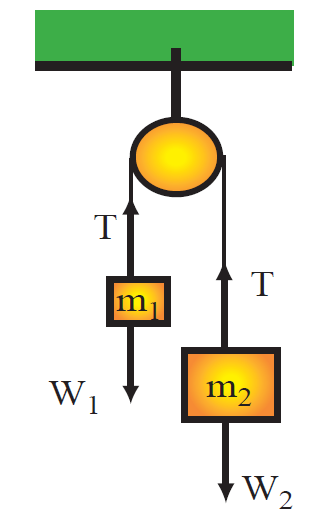
FIGURE 1.4 Atwood machine.
Solution The tension is the same throughout the rope; thus
T1 = T2 = T. Analyze forces in y direction on m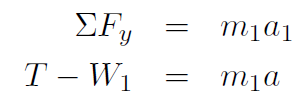1;
(1.1)
with a1 ´ a. Analyze forces in y direction on m2;
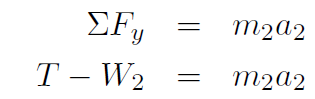
but if a1 = a then a2 = -a giving
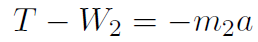(1.2)
Subtracting eqn. (1.2) from eqn. (1.1) gives
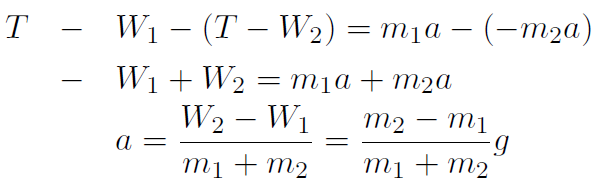
Thus a is positive if m2 > m1 and negative if m2 < m1.
الاكثر قراءة في الميكانيك
اخر الاخبار
اخبار العتبة العباسية المقدسة
