


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 20-1-2021
Date: 20-1-2021
Date: 23-3-2016
|
The maser and laser principle
The word "laser" is an acronym composed of the initial letters of "light amplification by stimulated emission of radiation". The laser principle emerged from the maser principle. The word "maser" is again an acronym standing for "microwave amplification by stimulated emission of radiation". The concept of stimulated emission stems from Einstein when in 1917 he derived Planck's law of radiation. It took nearly 40 years until it was recognized that this process can be used in a device producing coherent microwaves and in particular a new type of light laser light. The maser was proposed by Basov and Prokhorov (1954-1955) and by Townes (1954), who performed also experiments on that new device. We owe the extension of this principle to the optical region Schawlow and Townes (1958). One of the first proposals to use stimulated emission was contained in a patent granted in 1951 to V.A. Fabrikant, but being published in the official Soviet patent organ, it became available only in 1959. In 1977 patents on aspects of the laser principle were granted to Gould. Since his work had not been published it remained unknown to the scientific community. Because the laser principle is an extension of the maser principle, first the word "optical maser" had been proposed by Schawlow and Townes. However, nowadays the word "laser" is widely used because it is shorter. In order to understand the laser principle it is useful to first consider the maser principle. The device realizing this principle, which is again called maser, essentially consists of two components. On the one hand a cavity, on the other hand molecules which are in the cavity or which are injected into it. A cavity is practically a metal box of certain shape and dimension. In it specific electromagnetic waves with discrete wave-lengths can be formed (figs. 1.1 and 1.2). The corresponding standing waves shall be denoted in the following as "modes". They possess a discrete sequence of eigen2
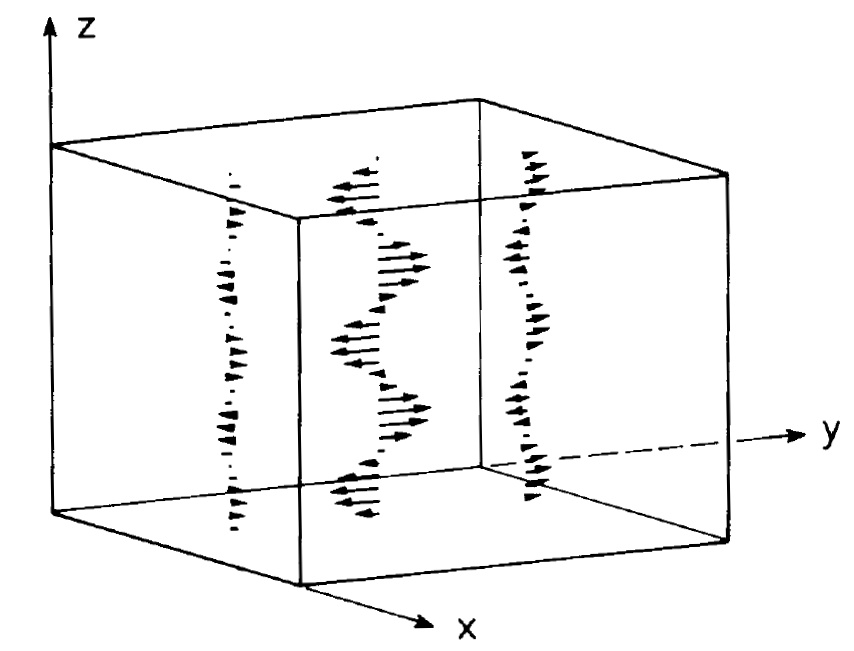
Fig. 1.1. Electro-magnetic field mode in a cavity. Local directions and sizes of the electric field strength are indicated by the corresponding arrows.
frequencies. These modes, which can exist in the cavity in principle, are now to be excited. To this end energetically excited molecules, e.g. ammonia molecules, are injected into the cavity. In order to understand the maser process, for the moment being it is only important to know that a transition between the excited state of the NH3 molecule and its ground state can take place which is accompanied by the emission of an electro-magnetic wave with quantum energy hv = Wi - Wf, where u is the frequency of the emitted wave, whereas Wi and Wf are the energies of the initial and final
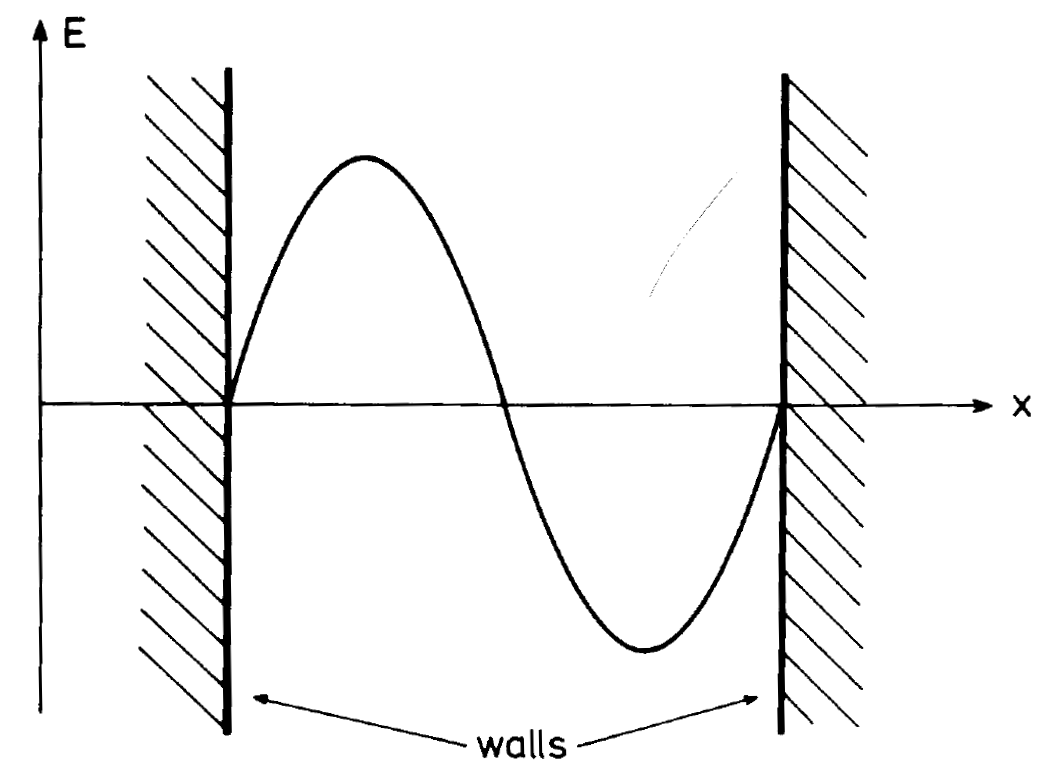
Fig. 1.2. Standing electric wave between two ideally conducting walls.
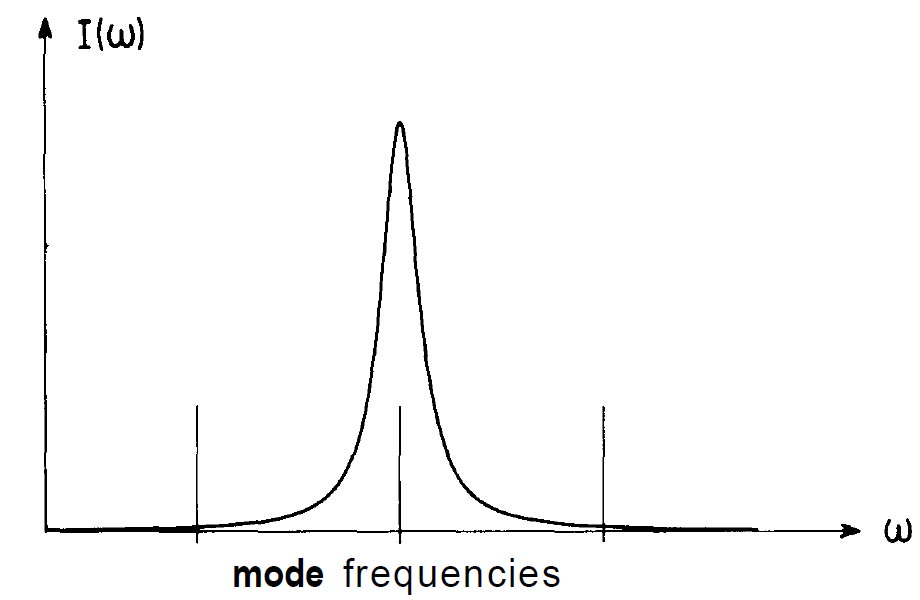
Fig. 1.3. Emission intensity of a molecule versus circular frequency. In most cases, in the microwave region the mode frequencies are so far apart that only one frequency comes to lie within the emission line.
state of the molecule, respectively. As we know, excited atoms or molecules can be stimulated to emit light quanta if one or several quanta of the electro-magnetic field are already present, and the whole process is called stimulated emission. By means of excited molecules in the cavity, a specific mode can be amplified more and more by stimulated emission. In order to achieve an efficient energy transfer from the molecules to the electro-magnetic field, the frequency of the molecular transition must coincide with the frequency of the mode to be amplified. More precisely speaking, it is necessary that the mode frequency lies within the line width of the molecular transition. With respect to the molecules used in the maser we can achieve the amplification of a specific mode by choosing the dimensions of the microwave cavity correspondingly. In this way only one frequency falls into the line-width whereas all other mode frequencies lie outside of it (fig. 1.3). Schawlow and Townes suggested to extend the maser principle to the optical region by using optical transitions between electronic levels of atoms. When one tries to realize the laser principle, fundamental new problems arise as compared to the maser. These problems stem from the fact that the light wave-length is small compared to a cavity of any reasonable dimension. Therefore in general the distance between different mode frequencies becomes very small so that very many modes come to lie within the frequency range of the atomic transition (fig. 1.4). Therefore a suitable mode selection must be made. One possibility consists in omitting the side walls of the resonator and to use only two mirrors mounted in parallel at two opposite sides. The thus resulting Fabry-Perot resonator, which was suggested by
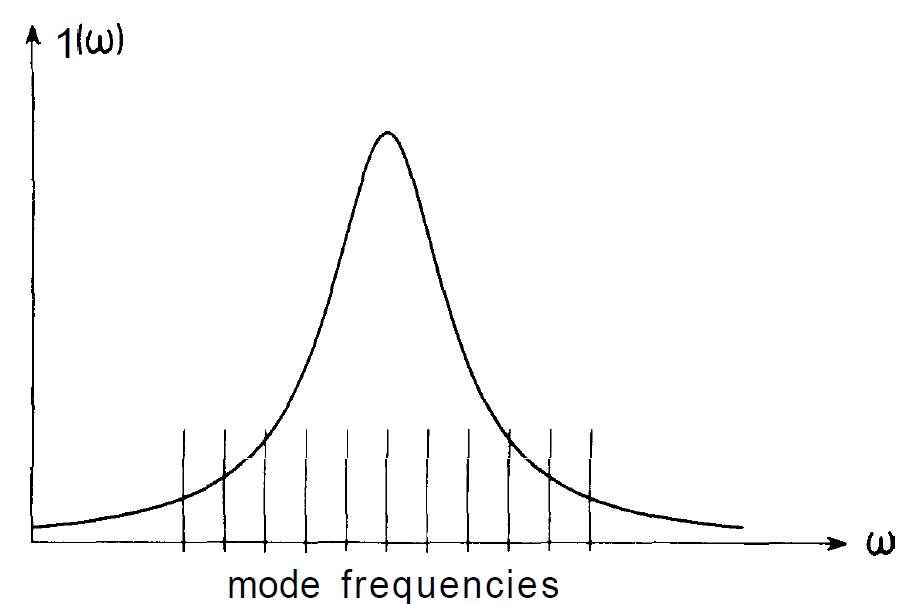
Fig. 1.4. Example for the positions of mode frequencies in the optical region. In general many frequencies come to lie within an emission line.
Schawlow and Townes, and Prokhorov and Dicke, makes a mode selection possible in two ways. Let us consider figs. 1.5 and 1.6. Before the laser process starts, the excited atoms emit light spontaneously into all possible directions. On account of the special arrangement of the mirrors only those light waves can stay long enough in the resonator to cause stimulated emission of atoms, which are sufficiently close to the laser axis, whereas other modes cannot be amplified. This mechanism is particularly efficient because only waves of the same direction, wave-length, and polarization are amplified by the stimulated emission process. In this way the Fabry Perot interferometer gives rise to a strong discrimination of the modes with respect
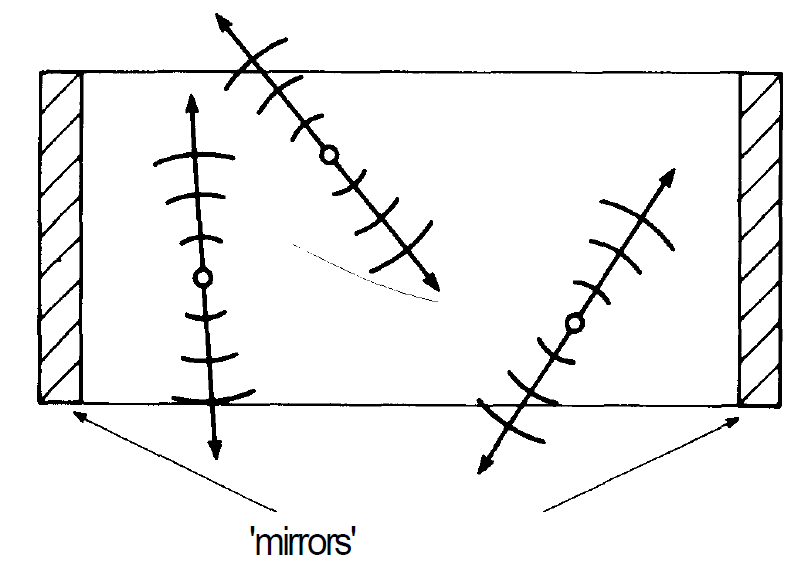
Fig. 1.5. The excited atoms in the laser resonator can radiate light into all directions. Waves which do not run in parallel to the laser axis, leave the resonator quickly and do not contribute to the laser process.
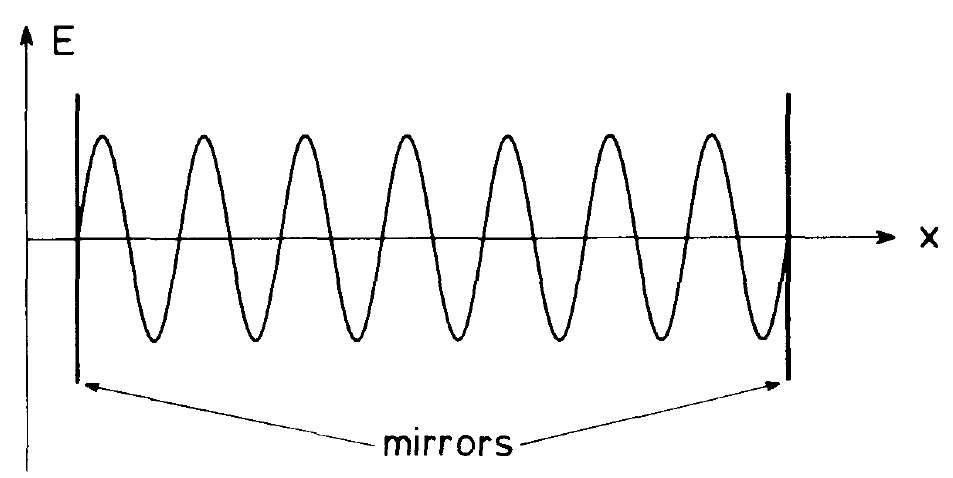
Fig. 1.6. The electric field strength of a standing axial wave in the laser resonator.
to their lifetimes. Furthermore the mirror arrangement can support only those axial modes for which
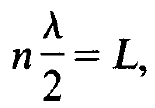
where A is the wave length, L the distance between the mirrors, and n an integer. Even under these circumstances quite often still many frequencies may exist within an atomic line-width. The final mode selection, often the selection of a single mode, is achieved by the laser process itself as we shall demonstrate in this book. The first experimental verification of the laser principle in 1960 is due to Maiman, who used ruby, a red gem. Since then laser physics has been mushrooming and it is still progressing at a rapid pace. Practically each year new materials or laser systems are discovered and still important tasks are ahead of us, for instance the extension of the laser principle into the x-ray and y-ray region. Today a great many laser materials are known and we shall briefly discuss some typical.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|