


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-11-2016
Date: 13-11-2016
Date: 12-11-2016
|
Died: 3 January 1892 in Breslau, Germany (now Wroclaw, Poland)
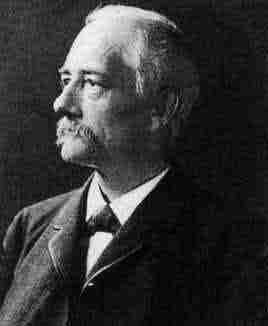
Heinrich Schröter's father was a respected merchant who became head of the College of Commerce in Königsberg. Heinrich was the eldest of his parents three sons. His primary education was at a private school then, when he was eleven years old, he entered the Altstädtischen Gymnasium in Königsberg. There he proved himself a diligent and conscientious pupil and, from the third form onwards, he began reading mathematics books. He was fortunate to have an outstanding teacher of mathematics, Professor Müttrich, several of whose pupils went on to become leading mathematicians. Schröter quickly learnt the foundations of the differential calculus and he decided that he wanted to apply mathematics. With expertise in technical drawing and constructing models, he thought that perhaps an occupation as a surveyor would suit him. He graduated from the Gymnasium in 1845 but, inspired by Müttrich, quickly changed his mind about his future profession and decided to study mathematics and physics at university. In fact Schröter was the first of a number outstanding mathematics pupils at the Königsberg Gymnasium, all influenced by Müttrich; Rudolf Lipschitz, Carl Neumann, and Alfred Clebsch were three to four years behind Schröter.
Returning to his native city, he entered the University of Königsberg to study mathematics and physics. The University of Königsberg had become a leading centre for mathematics during the years that Carl Jacobi worked there but he left for Berlin in June 1844 shortly before Schröter began his studies. However Königsberg still had excellent mathematicians in Friedrich Richelot and Otto Hesse who had both been students of Jacobi. Richelot was a worthy successor to Jacobi and continued to work in his spirit while Hesse continued Jacobi's algebraic work making fundamental contributions to the algebraic treatment of analytic geometry. Another outstanding mathematician at Königsberg at this time was Franz Neumann who had begun working there three years before Schröter was born but was at the peak of his creativity in the 1840s. Among these inspiring teachers it was Richelot who influenced Schröter most, introducing him to Jacobi's work on function theory.
Schröter graduated from Königsberg in 1848 after which he spent two years doing voluntary military service in the artillery before he began to undertake research for his doctorate at the University of Berlin. At Berlin he was taught by Lejeune Dirichlet and Jakob Steiner. He attended courses by Dirichlet on number theory and on differential equations which influenced Schröter's teaching for the whole of his career but it was Steiner who was a major influence on Schröter's research. Partly this influence was through the courses Steiner delivered, but his greatest influence on Schröter was through personal contacts. However his doctorate was obtained from Königsberg on 13 July 1854 for his dissertation on the theory of elliptic functions De aequationibus modularibus which was supervised by Richelot. Immediately after graduating, Schröter took the state examinations to become a Gymnasium mathematics teacher but quickly decided on an academic career. He submitted his habilitation thesis Über die Entwicklung der Potenzen der elliptischen Transcendenten Q und die Teilung dieser Functionen to the University of Breslau in the autumn of 1855.
After lecturing at the University of Breslau as a dozent, he become an extraordinary professor there in 1858. On 8 August 1860, he married Clara Rodewald, the daughter of a lawyer from Breslau; they had four children. The chair at Breslau had been held by Eduard Kummer until 1855 when he went to Berlin and, following his departure, the chair was filled by his student Ferdinand Joachimsthal. Schröter was a colleague of Joachimsthal until his death in 1861 when Schröter succeeded to the Breslau chair. In the following year Rudolf Lipschitz was appointed as extraordinary professor at Breslau and Schröter, Lipschitz and M Frankenheim jointly founded a seminar in mathematics and mathematical physics (for more details, see [6]). Schröter remained in Breslau for the rest of his life despite being offered another chair. When Alfred Clebsch left Giessen to take up the chair at Göttingen in 1868, Schröter was offered the Giessen chair but he turned it down. His last few years were badly affected by ill health and he suffered from paralysis.
Schröter created at Breslau the leading centre for synthetic geometry. His career in Breslau showed how strongly he had been influenced by Steiner. His first paper Über die Erzeugnisse krummer projektivischer Gebilde (1857) built on work by Steiner in a paper he published in January 1856. His next paper, however, Ueber die Raumcurven dritter Klasse und dritter Ordnung (1859) built on work by Chasles in a paper he published in 1857. In 1861 Schröter published Ueber Modulargleichungen der elliptischen Functionen, Auszug aus einem Schreiben an Herrn L Kronecker. After Steiner's death in 1863 he took over the publication of his posthumous manuscripts, particularly those which were related to the application of the theory of conic sections to projective curves. He edited his transcripts of Steiner's lectures on synthetic geometry which he interweaved with other material by Steiner, together with his own improvements, to produce Jacob Steiner's Vorlesungen über synthetische Geometrie (1867). This important work became the textbook for the synthetic geometry of conics with a second edition appearing in 1876 and a third edition in 1898 after Schröter's death. Next we mention two papers on third-order curves, Ueber eine besondere Curve dritter Ordnung und eine einfache Erzeugungsart der allgemeinen Curven dritten Ordnung (1872) and Ueber Curven dritter Ordnung (1873). His next major book was Die Theorie der Oberflächen zweiter Ordnung und der Raumkurven dritter Ordnung als Erzeugnisse projectivischer Gebilde which he published in 1880. This work on the theory of second order surfaces and third order space curves continues Steiner's work. In 1888 Schröter published a book on third-order plane curves Die Theorie der ebenen Curven dritter Ordnung, auf synthetische Weise abgeleitet and in 1890 he published his major study on fourth-order space curves in Grundzüge einer rein geometrischen Theorie der Raumcurven vierter Ordnung erster Species.
Among his doctoral students at the University of Breslau were Rudolf Sturm (doctorate awarded in 1863 for the thesis De superficiebus tertii ordinis disquisitiones geometricae), Jakob Rosanes (doctorate awarded 1865) and Moritz Pasch (doctorate awarded in 1865 for the thesis De duarum sectionem conicarum in circulos projectione). Rudolf Sturm wrote the biographies [4] and [5] of Schröter.
Schröter was honoured for his contributions to synthetic geometry. He received the Steiner Prize from the Berlin Academy of Science on 6 July 1876 and, on 6 January 1881 he was elected to the Berlin Academy of Science. In [2] the opinions of Weierstrass and Kronecker on Schröter are discussed, these being reports on him as a candidate for election to the Academy. On 9 December 1882 he was elected a Corresponding Member of the Göttingen Academy of Sciences.
Finally we mentions Schröter's interests outside mathematics. He was an excellent musician, playing the violin to a high standard in a local amateur orchestra. He was also keen on gymnastics and for twenty-five years he was the head of the Old Breslau Gymnastics Club.
Articles:



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|