


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | THE PONTRYAGIN MAXIMUM PRINCIPLE-MAXIMUMPRINCIPLEWITH TRANSVERSALITY CONDITIONS |
|
|
|
Read More
Date: 10-7-2016
Date: 3-10-2016
Date: 9-10-2016
|
Consider again the dynamics
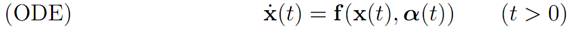
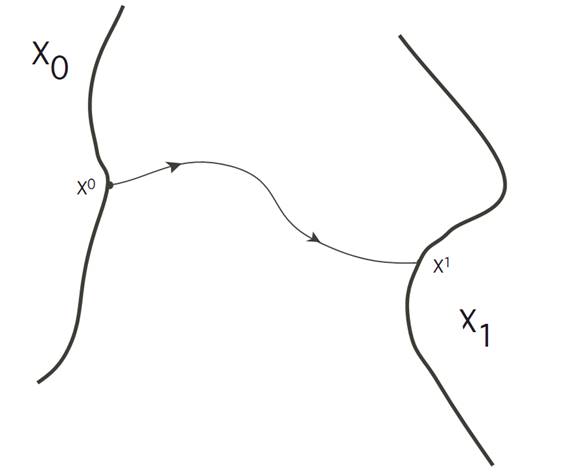
In this section we discuss another variant problem, one for which the initial position is constrained to lie in a given set X0 ⊂ Rn and the final position is also constrained to lie within a given set X1 ⊂ Rn.
So in this model we get to choose the starting point x0 ∈ X0 in order tomaximize
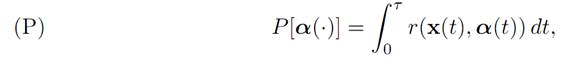
where τ = τ [α(.)] is the first time we hit X1.
NOTATION. We will assume that X0,X1 are in fact smooth surfaces in Rn.
We let T0 denote the tangent plane to X0 at x0, and T1 the tangent plane to X1 at x1.
THEOREM 1.1 (MORE TRANSVERSALITY CONDITIONS). Let α∗(.) and x∗(.) solve the problem above, with
x0= x∗ (0), x1= x∗ (τ ∗).
Then there exists a function p∗(.) : [0, τ ∗] → Rn, such that (ODE), (ADJ) and (M) hold for 0 ≤ t ≤ τ ∗. In addition,
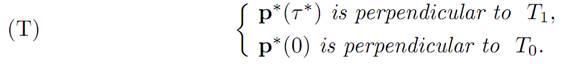
We call (T) the transversality conditions.
REMARKS AND INTERPRETATIONS. (i) If we have T > 0 fixed and
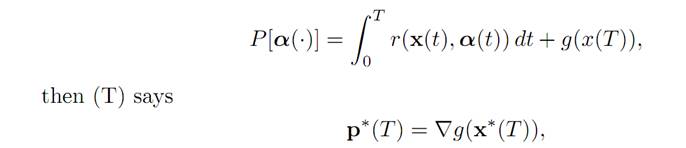
in agreement with our earlier form of the terminal/transversality condition.
(ii) Suppose that the surface X1 is the graph X1 = {x | gk(x) = 0, k = 1, . . . , l}.
Then (T) says that p∗(τ ∗) belongs to the “orthogonal complement” of the subspace T1. But orthogonal complement of T1 is the span of ∇gk(x1) (k = 1, . . . , l). Thus
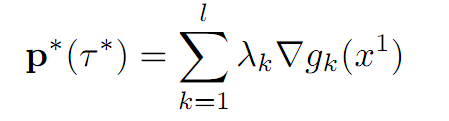
for some unknown constants λ1, . . . , λl.
References
[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.
[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.
[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.
[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.
[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.
[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.
[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.
[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.
[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.
[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).
[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.
[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.
[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.
[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.
[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.
[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.
[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.
[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.
[T] William J. Terrell, Some fundamental control theory I: Controllability, observability, and duality, American Math Monthly 106 (1999), 705–719.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
تضاريس شبيهة بـ"الجبنة السويسرية".. حفرة غامضة على المريخ
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|