


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 7-10-2016
Date: 5-10-2016
Date: 6-11-2016
|
Platonic Solids

There are five 3-D regular polyhedrons called the Platonic solids: the regular tetrahedron (4 faces), the regular hexahedron (cube), the regular octahedron (8 faces), the regular dodecahedron (12 faces), and the regular icosahedron (20 faces). All these solids have a twofold rotational symmetry axis through the center of each edge that is, a rotation about this axis by 180 degrees leaves the object looking the same as the initial view. But the regular tetrahedron does not have inversion symmetry.
If we intersect two identical regular tetrahedrons so their centers coincide, can the composite object have a twofold rotational symmetry axis? Can it have inversion symmetry?
Answer
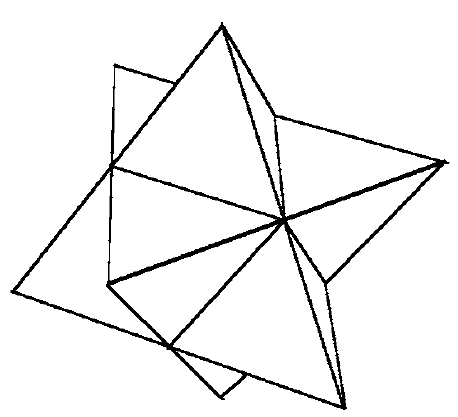
One must turn the second identical regular tetrahedron upside down and rotate by 30 degrees about the vertical axis before mathematically pushing them through each other to form a six vertex regular solid. Obviously these six vertices correspond to the vertices of a regular octahedron if the new object were placed inside one. However, the sides are not convex and flat. Our bi tetrahedron does have twofold symmetry axes even though the two tetrahedrons are rotated with respect to each other.
We might have asked you to place the two regular tetrahedrons face-to face in congruence so that the combined object has five vertices defining a triangular bi pyramid. There are now three twofold rotational symmetry axes, each one being through an edge of the joining faces. However, this bi pyramid is not a regular polyhedron.
If we were to extend the discussion to four spatial dimensions, there are six regular solid convex objects analogous to the five Platonic solids in three dimensions. The number of regular convex solids, called regular poly topes, does not increase with more spatial dimensions. Instead, all dimensions beyond four have only three regular convex solids.
The Platonic solids are special in many ways, but perhaps their most important mathematical property was pointed out by mathematician B. Kostant:
The ancient Greeks, especially the school of Plato, had great reverence for the regular polygons in the plane and regular solids in 3-space. The latter the tetrahedron, cube, octahedron, dodecahedron, and the icosahedron are often referred to as the Platonic solids. The Greeks believed that these regular figures were fundamental in the structure of the universe. If symmetry or its mathematical companion group theory is fundamental in the structure of the world, then one of the points of our lecture is the statement that the Greeks were absolutely right. That is, what we will be saying in a very profound way, the finite groups of symmetries in 3-space “see” the simple Lie groups (and hence literally Lie theory) in all dimensions.
One of us (F. P.) has proposed that the fundamental building blocks of matter, the leptons and quarks of the Standard Model of particle physics, are described mathematically by the specific rotational symmetries of the 3-D Platonic solids for the leptons and by their 4-D analogs for the quarks. The key arguments are that the mathematical symmetry groups for these regular solids are subgroups of the Standard Model symmetry group and that the lepton and quark mass ratios can be directly related to the ratios 1:108:1728 of the invariants of these subgroups. Whether the natural world mimics this fundamental mathematical behavior has yet to be determined by experiments at particle colliders.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|