


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 22-8-2016
Date: 11-8-2016
Date: 29-8-2016
|
Paramagnetism at High Temperature
a) Show that for a system with a discrete, finite energy spectrum εn, the specific heat per particle at high temperatures (τ >> εn for all n) is
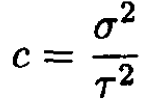
where σ is the spectrum variance
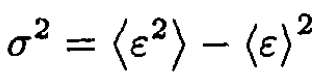
b) Use the result of (a) to derive the high-temperature specific heat for a paramagnetic solid treated both classically and quantum mechanically.
c) Compare your quantum mechanical result J = 1/2 for with the exact formula for c.
SOLUTION
a) The specific heat c of a system that has N energy states is given by
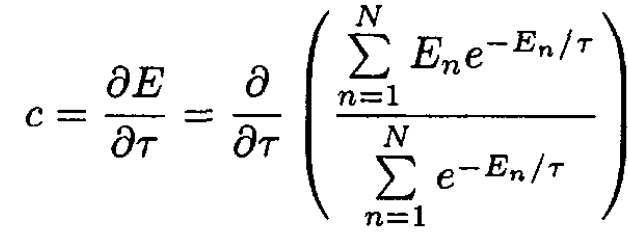 (1)
(1)
Using 1/τ = β, we may rewrite c:
 (2)
(2)
where we have used In (1 + x) ≈ x – x2/2. Note that, in general, the parameter βEn is not small (since it is proportional to the number of particles), but, subsequently, we obtain another parameter βε << 1.
b) For a classical paramagnetic solid:
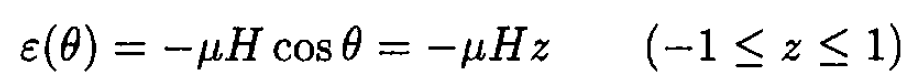
so

and we have
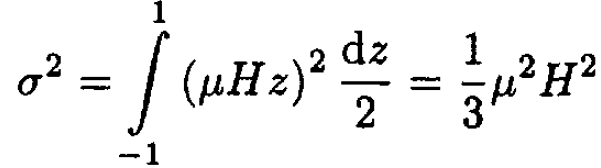 (3)
(3)
where dz/2 is the probability density. Therefore,
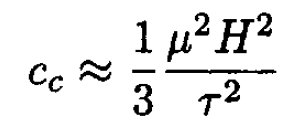 (4)
(4)
For the quantum mechanical case, ⟨ε⟩ = 0; there is an equidistant energy spectrum: Em = -gμBHm and
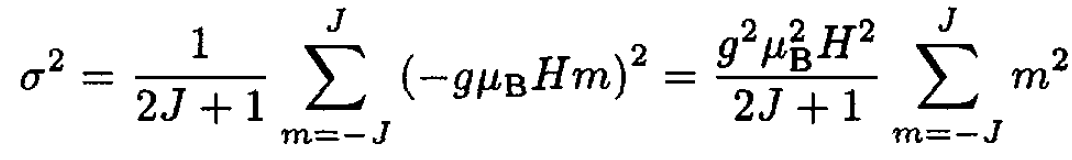 (5)
(5)
To calculate 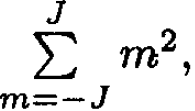 we can use the following trick (assuming J integer):
we can use the following trick (assuming J integer):
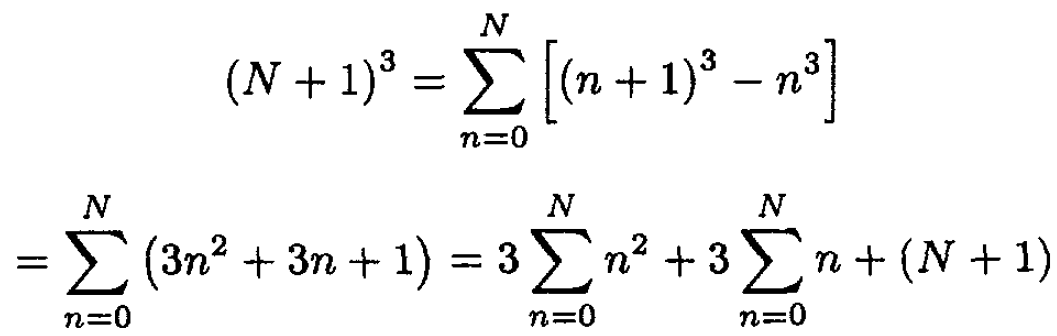 (6)
(6)
From (6) we have
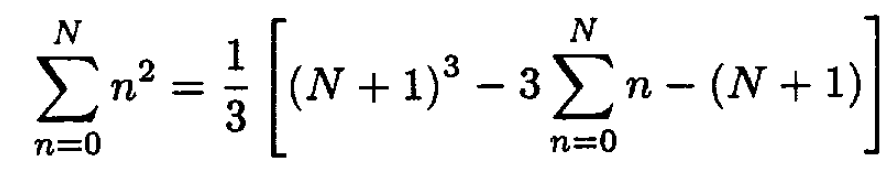 (7)
(7)
With the familiar sum
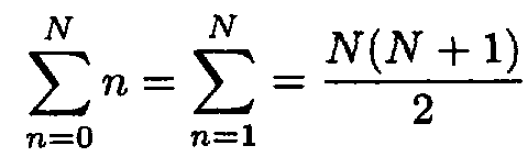
we arrive at
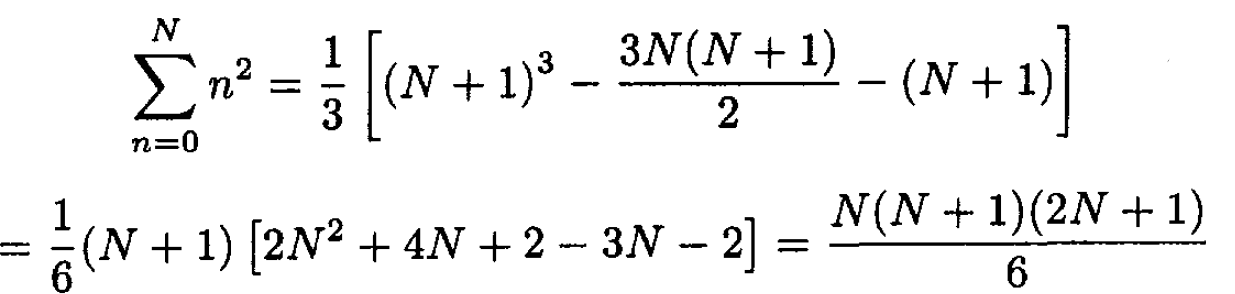 (8)
(8)
We wish to perform the sum from –J to J, so
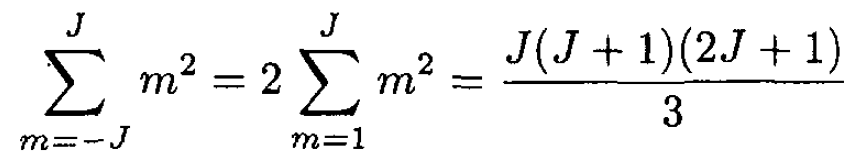
and (5) gives
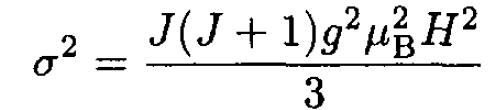 (9)
(9)
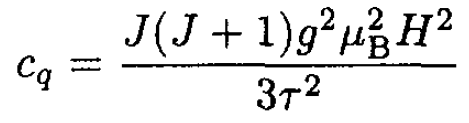 (10)
(10)
c) For J = 1/2,
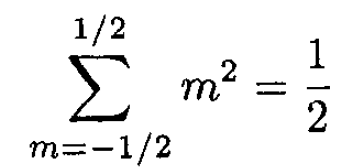
and
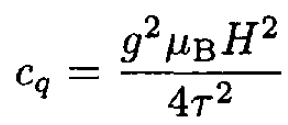 (11)
(11)
For J = 1/2:
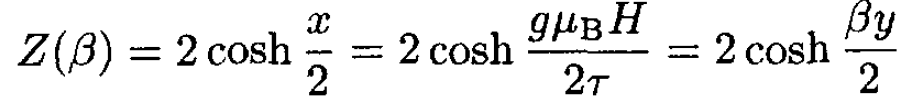 (12)
(12)
where y = gμBH. We then find
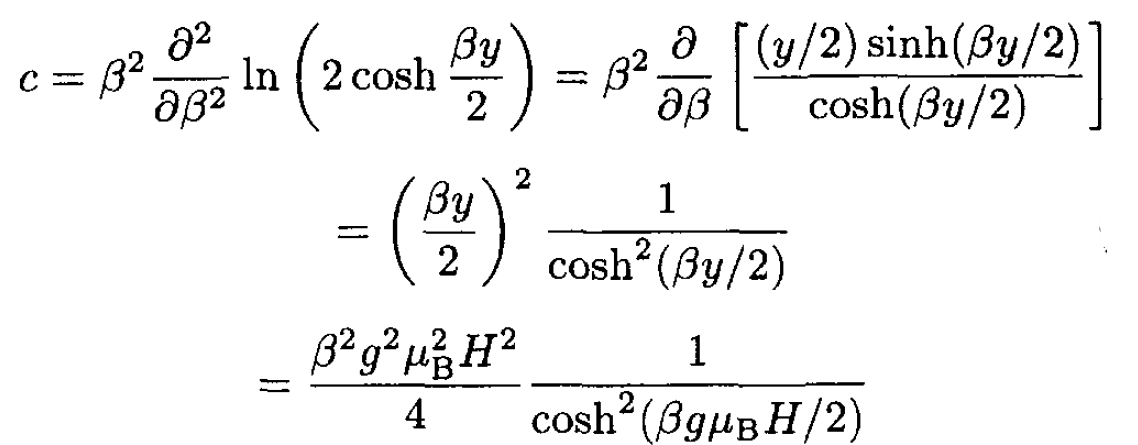 (13)
(13)
For τ → ∞, β → 0,
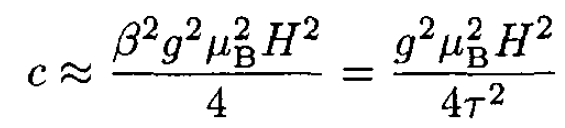
which coincides with (11).



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|