
Spherical Resistor
 المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 57
الجزء والصفحة:
part 1 , p 57
 11-8-2016
11-8-2016
 2206
2206
Spherical Resistor
A and B are opposite ends of a diameter AOB of a very thin spherical shell of radius a and thickness t. Current enters and leaves by two small
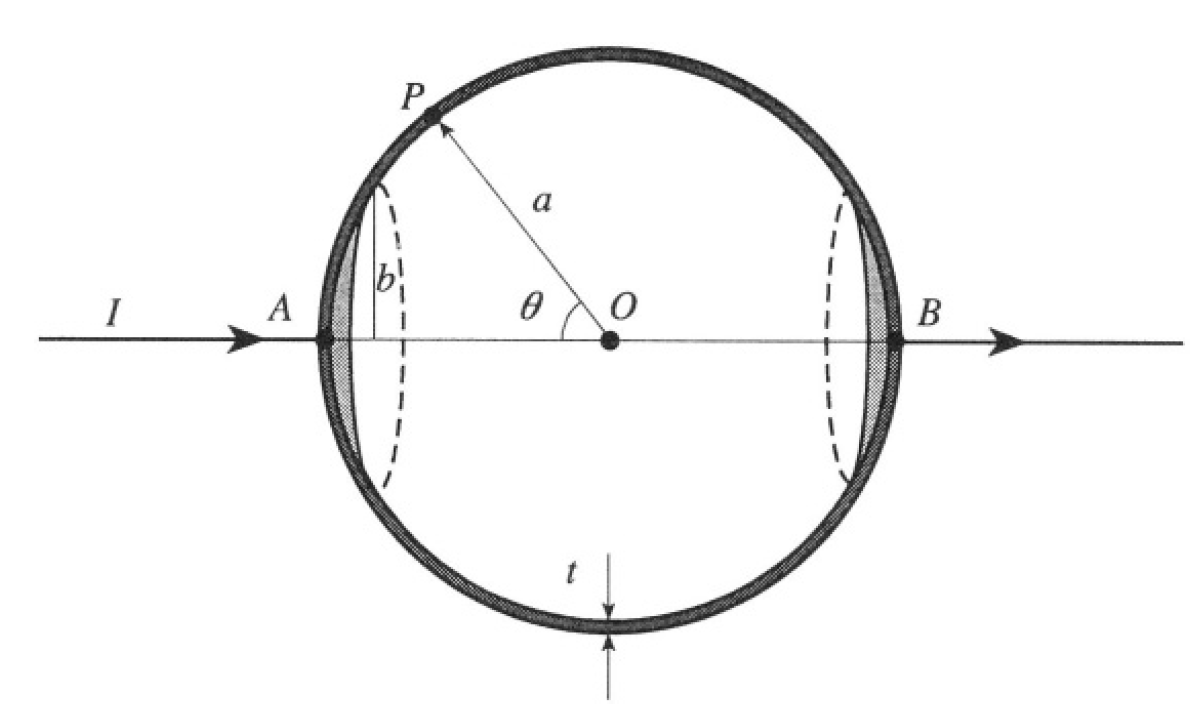
Figure 1.1
circular electrodes of radius b whose centers are at A and B (see Figure 1.1). If I is the total current and P is a point on the shell such that the angle POA = θ, show that the magnitude of the current density vector at P is proportional to (2πat sinθ)-1. Hence find the resistance of the conductor.
You may find this integral useful:
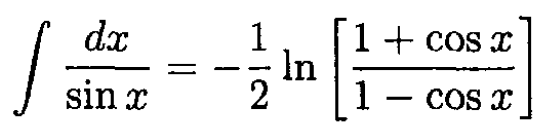
SOLUTION
The current density at point P may be written down immediately because of the cylindrical symmetry of the problem (see Figure 1.2). The current
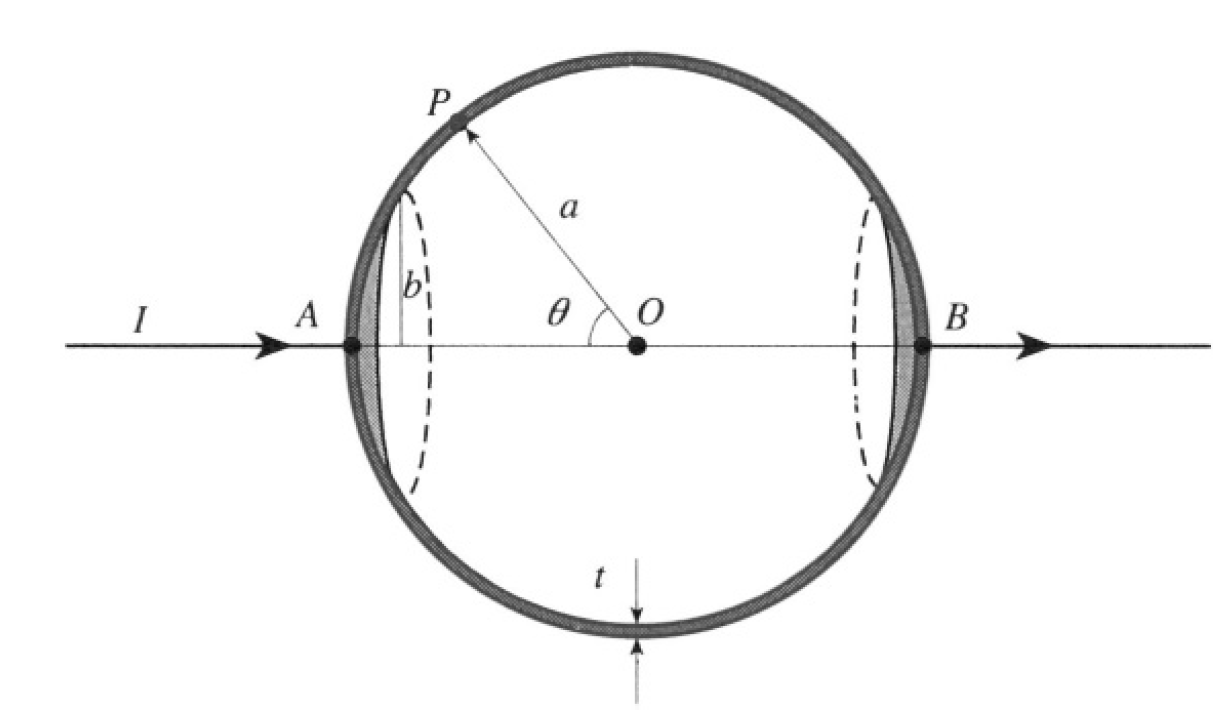
Figure 1.2
is divided evenly through 2π so that the current density J at each point in the spherical shell is
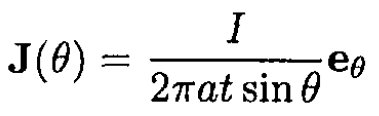 (1)
(1)
From the equation J = σE, where σ is the conductivity of the shell, we obtain
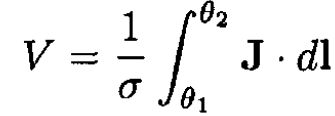
where V is the potential difference between the two electrodes. So
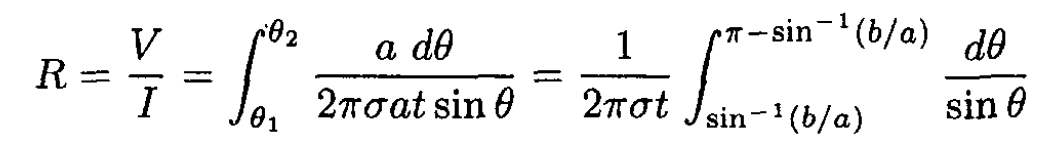 (2)
(2)
From the hint in the problem (which can by computed by using the substitution tan θ/2 = t) we can take the integral in (2):
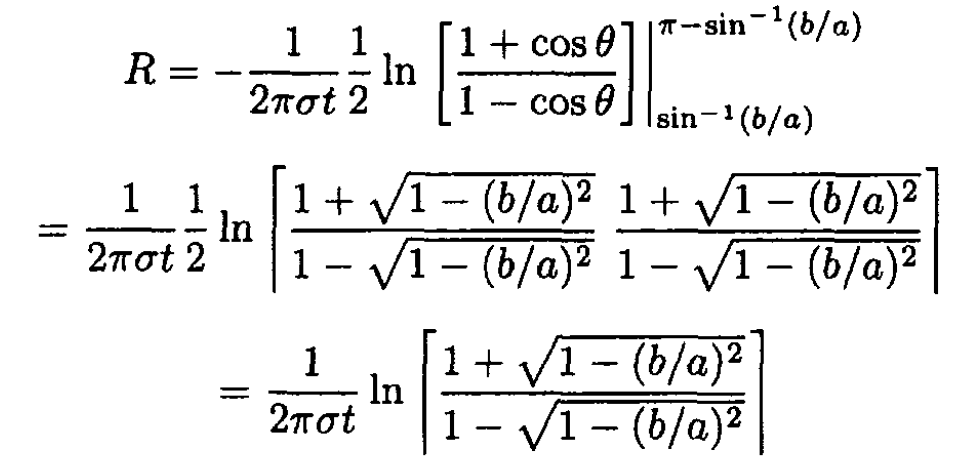
As the radius b of the electrodes goes to zero, the resistance goes to infinity!
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


