
Two Delta Function Potentials
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 54
الجزء والصفحة:
part 2 , p 54
 23-8-2016
23-8-2016
 1796
1796
Two Delta Function Potentials
A particle of mass m moves in a one-dimensional potential of the form
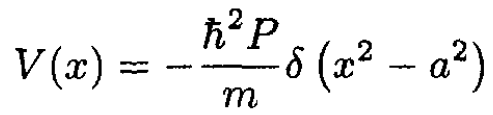 (i)
(i)
where P is a positive dimensionless constant and a has units of length. Discuss the bound states of this potential as a function of P.
SOLUTION
There are two delta function singularities, one at x = a and one at x = -a. The potential can be written in an equivalent way as
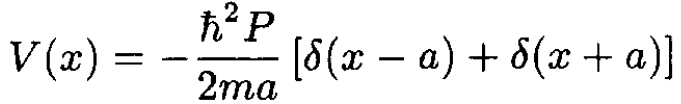 (1)
(1)
At each delta function we match the amplitudes of the eigenfunctions as well as the slopes, using a relation such as (3). A single, isolated, attractive, professional, delta function potential has a single bound state. We expect that a pair of delta function potentials will generally have one or two bound states.
The lowest energy state, for symmetric potentials, is a symmetric eigenfunction. The eigenvalue has the form E = -h2α2/2m, where α is the decay constant of the eigenfunction. The most general symmetric eigenfunction for a bound state is
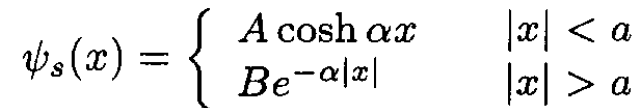 (2)
(2)
Matching at either x = ±a gives the pair of equations:
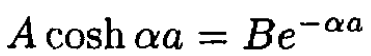 (3)
(3)
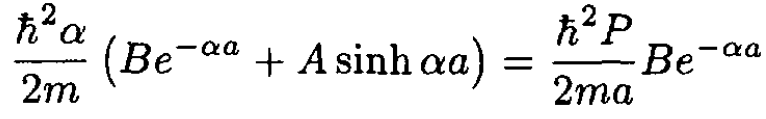 (4)
(4)
Eliminating the constants A and B gives the final equation for the unknown constant α:
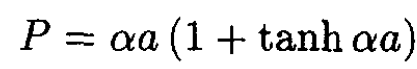 (5)
(5)
For large values of αa the hyperbolic tangent is unity, and we have the approximate result that P ≈ 2αa, which gives for large P the eigenvalue E ≈ -h2P2/8ma2. For small values of αa we see that P ≈ αa and E ≈ -h2P2/2ma2 This is always the lowest eigenvalue.
The other possible eigenstate is antisymmetric: it has odd parity. When the separate bound states from the two delta functions overlap, they combine into bonding and antibonding states. The bonding state is the symmetric state we calculated above. Now we calculate the antibonding state, which is antisymmetric:
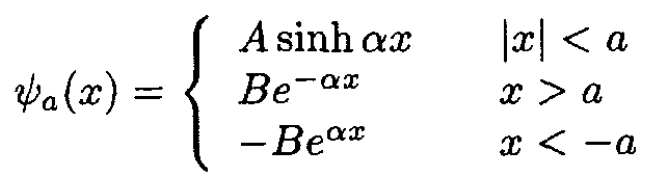 (6)
(6)
Using the same matching conditions, we find the two equations, which are reduced to the final equation for α:
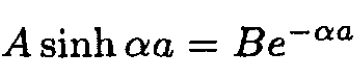 (7)
(7)
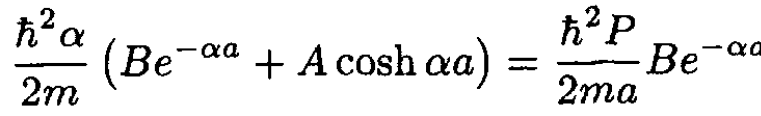 (8)
(8)
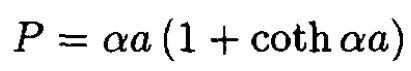 (9)
(9)
For large values of αa the hyperbolic cotangent function (coth) approaches unity, and again we find P ≈ αa and E ≈ -h2P2/8ma2. At small values of x the factor of x coth x → 1. Here we have x = αa, so we find at small values of αa that P → 1. The antisymmetric mode only exists for P > 1. For P < 1 the only bound state is the symmetric one. For P > 1 there are two bound states, symmetric and antisymmetric.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


