
Switched-on Field
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 59
الجزء والصفحة:
part 2 , p 59
 22-8-2016
22-8-2016
 1580
1580
Switched-on Field
Consider a simple harmonic oscillator in one dimension with the usual Hamiltonian
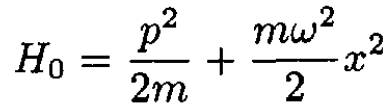 (i)
(i)
a) The eigenfunction of the ground state can be written as
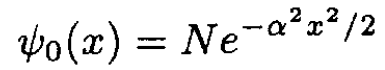 (ii)
(ii)
Determine the constants N and α.
b) What is the eigenvalue of the ground state?
c) At time t = 0, an electric field |E| is switched on, adding a perturbation of the form H' = e|E|x. What is the new ground state energy?
d) Assuming that the field is switched on in a time much faster than 1/ω, what is the probability that the particle stays in the ground state?
SOLUTION
a) Operate on the eigenfunction by the kinetic energy term in the Hamiltonian:
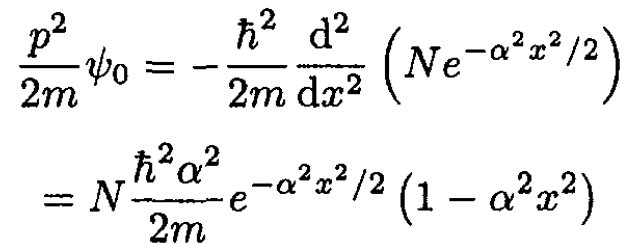 (1)
(1)
Consider the factor 1 - α2x2; the 1 must give the α2x2 eigenvalue and must cancel the potential energy. These two constraints give the identities
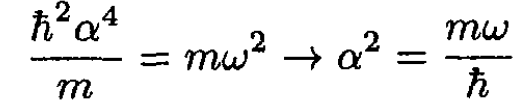 (2)
(2)
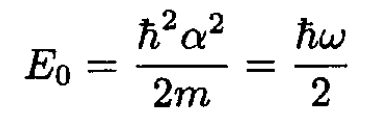 (3)
(3)
The normalization constant N is determined by
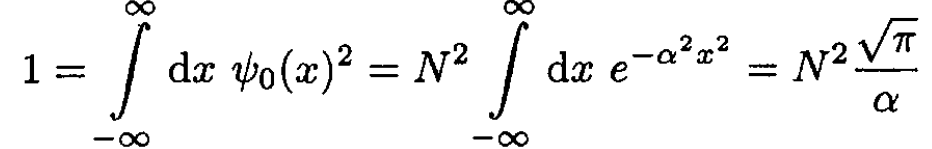 (4)
(4)
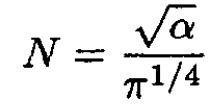 (5)
(5)
b) The solution is given above: E0 = hω/2.
c) After the perturbation e|E|x is added, the Hamiltonian can be solved exactly by completing the square on the x-variable:
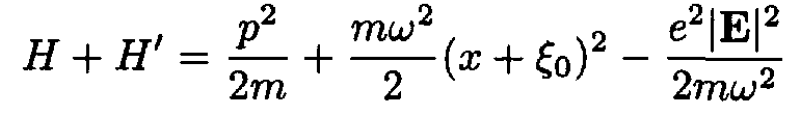 (6)
(6)
where the displacement ξ0 = e|E|/mω2. The new ground state energy and eigenfunction are
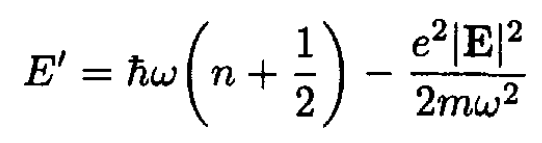 (7)
(7)
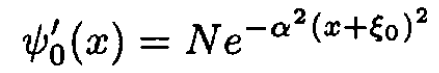 (8)
(8)
The harmonic oscillator vibrates about the new equilibrium point –ξ0 with the same frequency ω as before. The constants N and α are unchanged by
d) To find the probability that a particle, initially in the ground state, remains in the ground state after switching on the potential, we employ the sudden approximation. Here we just evaluate the overlap integral of the two eigenfunctions, and the probability is the square of this overlap:
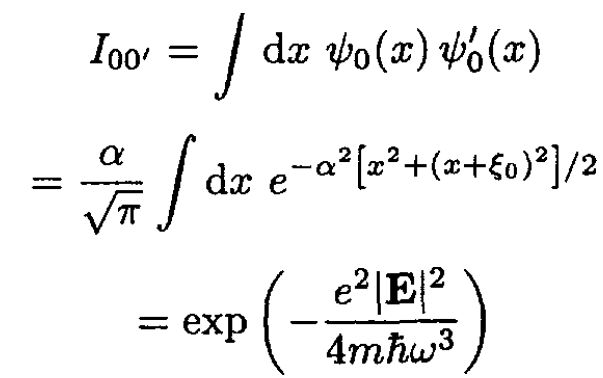 (9)
(9)
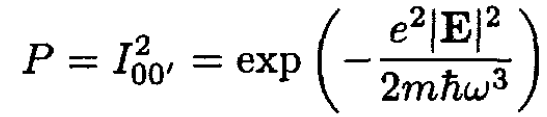 (10)
(10)
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


