
Scattering from Neutral Charge Distribution
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 77
الجزء والصفحة:
part 2 , p 77
 21-8-2016
21-8-2016
 1814
1814
Scattering from Neutral Charge Distribution
Consider the nonrelativistic scattering of a particle of mass m and charge e from a fixed distribution of charge ρ(r). Assume that the charge distribution is neutral: ∫d3r ρ(r) = 0; it is spherically symmetric; and the second moment, is defined as
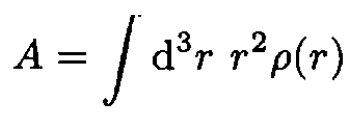 (i)
(i)
a) Use the Born approximation to derive the differential cross section dσ/dΩ for the scattering of a particle of wave vector k.
b) Derive the expression for forward scattering (θ → 0).
c) Assume that ρ(r) is for a neutral hydrogen atom in its ground state. Calculate A in this case. Neglect exchange effects and assume that the target does not recoil.
SOLUTION
a) The particle scatters from the potential energy V(r) which is related to the charge distribution
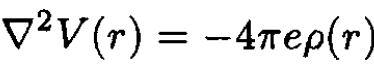 (1)
(1)
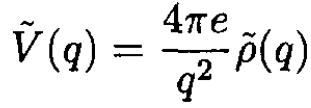 (2)
(2)
where 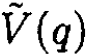 is the Fourier transform of V(r) and
is the Fourier transform of V(r) and 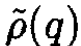 is the Fourier transform of ρ(r). The differential cross section in the Born approximation is
is the Fourier transform of ρ(r). The differential cross section in the Born approximation is
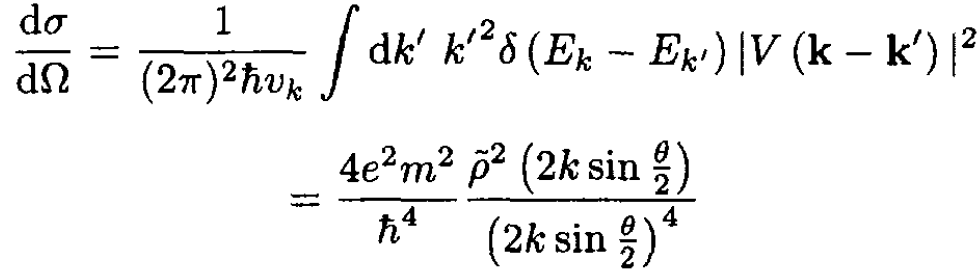 (3)
(3)
b) In forward scattering we take θ → 0. In order that the cross section have a non-divergent result in this limit, we need to find
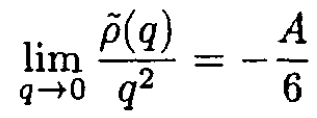 (4)
(4)
To obtain this result, we examine the behavior of 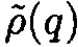 at small values of q:
at small values of q:
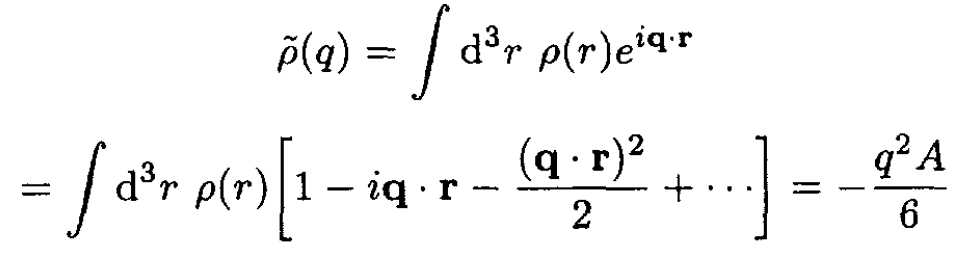 (5)
(5)
Consider the three terms in brackets: (i) the 1 vanishes since the distribution is neutral; (ii) the second term vanishes since the distribution is spherically symmetric; (iii) the last term gives an angular average (q . r)2 = (qr)2/3 and the integral of r2ρ is A. The cross section in forward scattering is
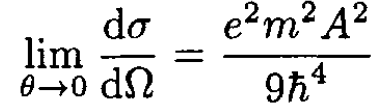 (6)
(6)
c) The charges in a hydrogen atom are the nucleus, which is taken as a delta function at the origin, and the electron, which is given by the square of the ground state wave function ѱ21s(r):
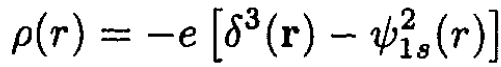 (7)
(7)
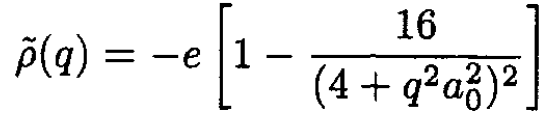 (8)
(8)
 (9)
(9)
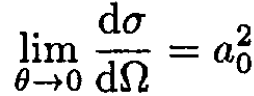 (10)
(10)
where a0 is the Bohr radius.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


