
Coupled Oscillators
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 58
الجزء والصفحة:
part 2 , p 58
 14-8-2016
14-8-2016
 1739
1739
Coupled Oscillators
Two identical harmonic oscillators in one dimension each have mass m and frequency ω. Let the two oscillators be coupled by an interaction term Cx1x2, where C is a constant and x1 and x2 are the coordinates of the two oscillators. Find the exact spectrum of eigenvalues for this coupled system.
SOLUTION
The Hamiltonian of the system is
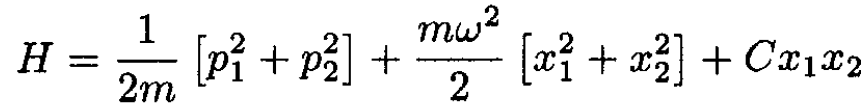 (1)
(1)
The problem is easily solved in center-of-mass coordinates. So define
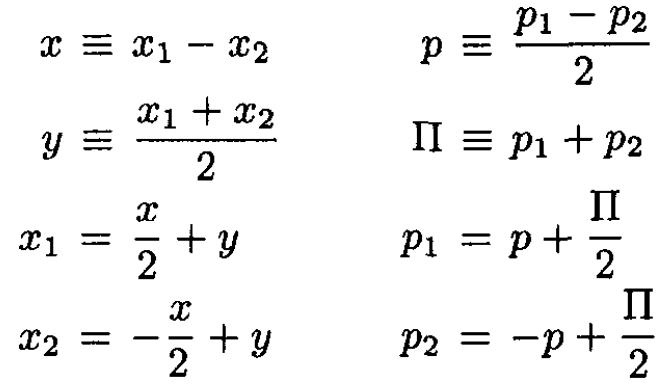 (2)
(2)
These new coordinates are used to rewrite the Hamiltonian. It now decouples into separate x- and y- parts:
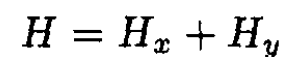 (3)
(3)
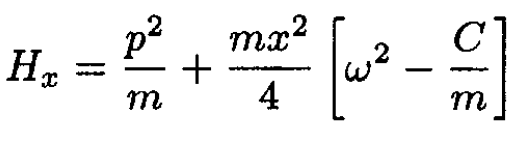 (4)
(4)
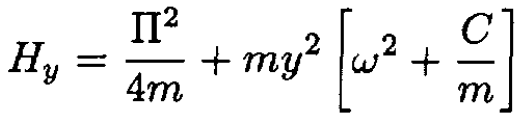 (5)
(5)
The x-oscillator has a frequency 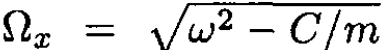 and eigenvalues hΩx (nx + 1/2), where nx is an integer. The y-oscillator has a frequency of
and eigenvalues hΩx (nx + 1/2), where nx is an integer. The y-oscillator has a frequency of 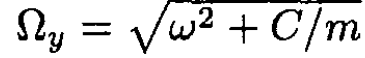 and eigenvalues hΩy (ny + 1/2), where ny is an integer.
and eigenvalues hΩy (ny + 1/2), where ny is an integer.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


