
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Attractive Delta Function Potential I
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 2 , p 52
14-8-2016
1795
Attractive Delta Function Potential I
A particle of mass m moves in one dimension under the influence of an attractive delta function potential at the origin. The Schrodinger equation is
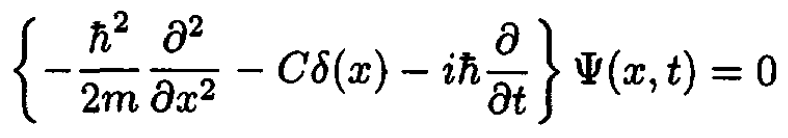 (i)
(i)
Figure 1.1
a) Find the eigenvalue and eigenfunction of the bound state.
b) If the system is in the bound state and the strength of the potential is changed suddenly C → C', what is the probability that the particle remains bound?
SOLUTION
a) The bound state is stationary in time: its eigenvalue is E (E < 0), and the time dependence of the wave function is Ψ(x, t) = ѱ(x) exp(-iEt/h). The equation for the bound state is
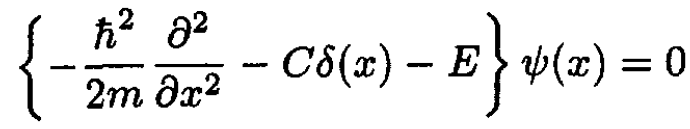 (1)
(1)
The bound state for x ≠ 0 has the form
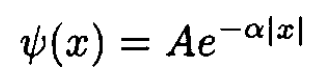 (2)
(2)
We have already imposed the constraint that ѱ(x) be continuous at x = 0. This form satisfies the requirement that ѱ(x) is continuous at the origin and vanishes at infinity. Away from the origin the potential is zero, and the Schrodinger equation just gives E = -h2α2/2m. A relation between C and E is found by matching the derivatives of the wave functions at x = 0. Taking the integral of (1) between 0+ and 0- gives
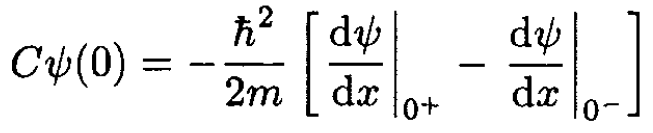 (3)
(3)
Applying (3) to (2) gives the relations
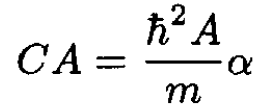 (4)
(4)
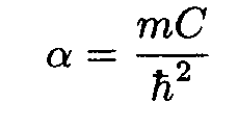 (5)
(5)
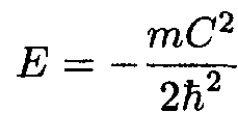 (6)
(6)
We have found the eigenvalue for the bound state. Note that the dimensions of C are energy × distance, which makes the eigenvalue have units of energy. Finally, we find the normalization coefficient A:
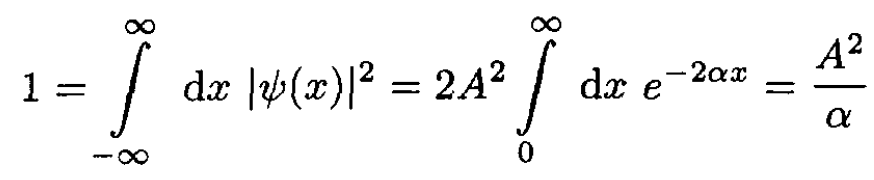 (7)
(7)
b) When the potential constant changes from C → C', the eigenfunction changes from ѱ(x) → ѱ'(x), where the prime denotes the eigenfunction with the potential strength C'. In the sudden approximation the probability P0 that the particle remains in the bound state is given by
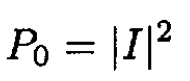 (8)
(8)
where
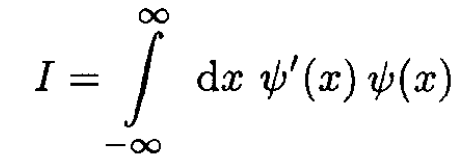 (9)
(9)
Substituting (2) into (9) and using the result of (7), we obtain
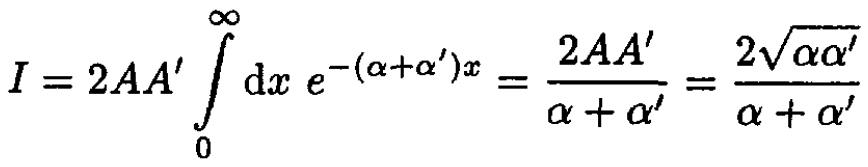 (10)
(10)
Finally, using (5) yields
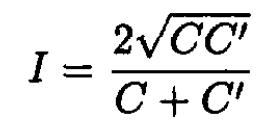 (11)
(11)
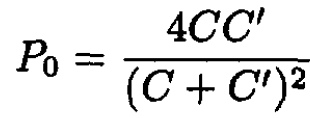 (12)
(12)
It is easy to show that P0 ≤ 1 as required by particle conservation. If C = C', then P0 = 1 since there is no change, and the particle must stay in the bound state.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















